KONKRET MATEMATIK

af H. B. Hansen

Det fleste der har lært "højere" matematik er opdraget med de reelle tal, sådanne sager som kontinuitet, differentialregning og integralregning. Det er imidlertid ikke lige netop den slags matematik man har mest brug for når man beskæftiger sig med datalogi. I datalogien er alt diskret - selv de reelle tal repræsenteres jo som diskrete data, og regning med reelle tal er derfor en hel disciplin for sig, kaldet numerisk matematik.

Når man begynder at interessere sig for algoritmer og deres analyse kommer man rigtig i bekneb, for der slår den kontinuerte matematik overhovedet ikke til. Før 1968 famlede vi os frem, men det år udkom det første bind af Knuths bog: The Art of Computer Programming, og dér åbenbaredes den matematik der var brug for (Knuth(1968)). Matematikerne har kendt denne matematik i hundredvis af år, men den er i det store og hele forblevet deres private gebet, indtil vi dataloger fik det praktiske behov. Desværre viser det sig at den særlige diskrete matematik der er tale om, er vanskelig at tilegne sig for almindelige mennesker der er opfostret i den kontinuerte tradition, og det har sikkert været et problem for mange dataloger foruden mig selv.

Nu er der imidlertid udkommet en lærebog, Graham(1989), i specielt denne form for matematik; den hedder "Konkret Matematik", hvilket er en sammentrækning af kontinuert og diskret matematik. Det var en stor inspiration for mig at læse denne bog; den gav mig et skub fremad i min forståelse og beherskelse af algoritmeanalysens matematik, og derfor fik jeg lyst til at delagtiggøre andre i nogle af mine oplevelser med den konkrete matematik. Dette essay handler altså om matematik, men jeg vil forsøge at relatere det så meget som muligt til datalogiske problemstillinger. Der er ikke noget nyt i det jeg siger, så dette er blot en appetitvækker der måske kan inspirere én og anden til at gå videre i den konkrete matematiks fascinerende verden på egen hånd.

Rekursioner

Men lad os med det samme kaste os ud i en typisk problemstilling hvor den konkrete matematik kan finde anvendelse. Der findes en simpel sorteringsmetode der kaldes "indsættelse"; den benytter samme princip som kortspillere der ordner de kort de får på hånden. Man sidder med n-1 kort der i forvejen er ordnet i rækkefølge efter farve og størrelse, og får så det n'te kort, der skal ind i denne rækkefølge.

Datalogisk set er situationen den at man har et array A, hvor de første n-1 elementer er en stigende rækkefølge af hele tal, og nu ankommer et nyt tal som skal ind i A på den rette plads. Det kan gøres ved hjælp af følgende algoritme, skrevet i Pascal:

i := n-1;

while (i > 0) and (A[i] > tal) do begin

A[i+1] := A[i]; i := i - 1

end;

A[i+1] := tal; n := n + 1;

Problemet er nu hvor mange gange while-løkken gennemløbes når alle tallene skal sorteres (algoritmen ovenfor må udføres for alle tallene efter tur).

Nu er denne algoritme så simpel at man nok kan besvare dette spørgsmål uden store matematiske udfoldelser, men lad mig gøre det på den typiske konkrete måde for demonstrationens skyld. Den konkrete matematiker tænker således:

Lad antallet af operationer når der er n elementer i A være a_n. For at komme til dette antal må vi først sortere n-1 tal (ved hjælp af indsættelse), og derefter anbringe det n'te tal (sådan ville man faktisk programmere metoden i fx Prolog). Sortering af de n-1 første tal bruger a_n-1 operationer, og anbringelse af det n'te tal vil i gennemsnit kræve ca. n/2 gennemløb af while-løkken, hvis alle tal er lige sandsynlige. En gennemsnitsbetragtning siger derfor at der gælder følgende sammenhæng:

a₁ = 0

Sådan et sæt ligninger kaldes en rekursion. En rekursion består altid af en ligning der udtrykker en generel sammenhæng, samt en eller flere startbetingelser. Opgaven består nu i at finde et afsluttet udtryk for a_n, dvs. en formel man blot kan sætte værdien af n ind i.

Man er ude efter den afsluttede formel for a_n fordi sådan en siger meget mere om hvordan processen arter sig end en tabel over funktionsværdierne (og så fylder den meget mindre), men sådan set kunne man godt nøjes med rekursionen hvis man vidste hvor mange elementer der skulle sorteres, for man kan starte med startbetingelsen og arbejde sig skridtvis frem, således:

a₁ = 0

, o.s.v.

Vi ser at der fremkommer en talfølge af følgende udseende:

0, 2, 5, 9, 14, ...

hvor jeg kun har taget tællerne i brøkerne med. Studiet af sådanne talfølger er en vigtig del af den konkrete matematik. Ofte er kendskab til en talfølge nok til at løse opgaven at finde a_n, for der findes nemlig en bemærkelsesværdig bog der indeholder en fortegnelse over alverdens talfølger, med angivelse af hvor man kan søge yderligere oplysninger om talfølgen, og/eller angivelse af det n'te led. Blandt dyrkere af den konkrete matematik kaldes den blot for Sloane, fordi det er en fyr ved navn Sloane der har samlet alt materialet og udgivet det, Sloane(1973). Slår vi op i Sloane finder vi, som talfølge nr. 522:

1, 2, 5, 9, 14, 20, 27, ...

med angivelsen n(n+3)/2. Nu skal man passe lidt på, for det er ikke sikkert at Sloanes talfølge er præcis den man søger. Han angiver ikke eksplicit hvordan han nummererer elementerne, og det første element hos Sloane er et 1-tal i stedet for et nul. Der er noget mystisk ved dette 1-tal. Det er som om det skal være det 0'te element, for det næste tal, 2-tallet, stemmer hvis man sætter n = 1: 1*(1+3)/2 = 2. På den anden side kan 1-tallet alligevel ikke være det 0'te element, for det stemmer ikke med formlen. Disse mærkværdigheder skyldes den måde talfølgerne er systematiseret på i Sloane, således at det blive let at slå op, og man skal derfor i nogle tilfælde foretage visse justeringer af de angivne formler for at få sin egen opgave til at stemme. I vores tilfælde ser vi at man skal forskyde tallene én position således at Sloanes 2-tal for n = 1 bliver til vores 2-tal for n = 2. Løsningen er derfor:

Man kan overbevise sig om at det er den rigtige løsning man har fundet ved at benytte et induktionsbevis.

Startbetingelse: n = 1 giver a₁ = 0, ok.

Induktionsskridt:

Højre side: ,

er lig med venstresiden, QED.

Men hvad gør man hvis ens talfølge ikke findes i Sloane? Så må vi løse rekursionen. I simple tilfælde som det foreliggende kan man "se" sig frem til løsningen ved hjælp af en proces der kaldes teleskopering (efter de gamle søkikkerter, der kunne trækkes ud og klappes sammen):

Da a₁ = 0 findes løsningen altså som summen:

½*(2 + 3 + 4 + ... + (n-1) + n)

Parentesen er en differensrække med n-1 led, så summen bliver:

som før.

Dette resultat kan generaliseres. En rekursion af formen:

a_n = a_n-1 + f(n)

a_p = q

a_k = 0 for alle k < p

hvor f(n) er en kendt funktion af n, har løsningen

a_n = q + f(p+1) + f(p+2) + f(p+3) + ... + f(n)

eller skrevet som den konkrete matematiker foretrækker:

Man ser her at optælling er en vigtig operation ved analyse af algoritmer. Derfor er det vigtigt for en datalog at beherske operationen summation. Dette gælder ikke blot for rekursioner af denne simple form. I alle tilfælde hvor man itererer sig frem i en rekursion ender man med én eller flere summer.

Summer

For summer gælder der nogle regneregler der i og for sig er indlysende, men som alligevel kan forvirre begyndere. Her er de vigtigste:

Distributive lov:

Associative lov:

Kommutative lov:

hvor p(k) betegner en permutation af værdierne i K (se nedenfor).

Den distributive lov siger at man kan sætte en fælles faktor uden for parentes (eller gange ind). Den associative lov siger at summen af en sum er lig med summen af det ene led plus summen af det andet led. Endelig siger den kommutative lov at addendernes orden er ligegyldig.

Her må jeg nok sige et par ord om notationen. Grænserne for det løbende indeks for en summation angives som et logisk prædikat under summationstegnet. I ovenstående summer er k det løbende indeks, og K er den værdimængde som dette indeks skal tage værdier fra. Operatoren Î er medlemsoperatoren, med betydningen "alle". Hvis fx K = {5,3,2} så står udtrykket for summen a₅ + a₃ + a₂.

Prædikatet p(k) i den kommutative lov skal betyde "en permutation af K", og denne lov siger altså blot at ovenstående eksempel også kan beregnes som a₂ + a₃ + a₅, eller en hvilken som helst anden orden af addenderne.

Denne prædikatnotation for summationsindeks er praktisk fordi man ofte har brug for at angive andre betingelser end lige netop heltalsintervaller (Eksempel:), samt fordi man næsten altid har behov for at operere på grænserne for en summation når man regner. Fx gælder der en meget fundamental regel der siger at navnet for summationsindeks er irrelevant, altså:

Som eksempel på dette vil jeg vise hvordan Gauss’ berømte argument for summen af en differensrække tager sig ud i den konkrete matematiks sprog.

Opgave: find

Vi skriver først

og bruger derefter navngivningsreglen, idet vi erstatter k med n-k :

Betingelsen for k kan omformes til:

altså de samme grænser som før (det er blot summation "bagfra"). Men nu kan vi bruge den associative lov på de to udtryk for S:

Størrelsen (2a + bn) afhænger ikke af k; den er konstant og kan sættes uden for summationstegnet ifølge den distributive lov. Derfor får vi:

Vi har altså fundet formlen:

eller i ord: summen af en differensrække er lig med det halve antal led gange summen af første og sidste led.

Man kan også finde summen af en kvotientrække ved manipulation af sumformler. Her benytter man et generelt princip der hedder perturbation; det går ud på at lægge et ekstra led til den søgte sum, og samtidig trække det første led ud. Se her:

Opgave: find

Ved at løse denne ligning med hensyn til S får man:

hvilket er den kendte formel for summen af de n første led i en kvotientrække med kvotient q ¹1. Hvis q = 1 fås S = a(n+1), hvilket ses umiddelbart af det oprindelige udtryk for S. Mange summer kan findes ved hjælp af perturbation.

Differenser

Der findes en uhyre interessant og nyttig analogi mellem de diskrete talfølger vi her beskæftiger os med, og de kontinuerte funktioner man arbejder med i differential- og integralregning. Som bekendt defineres differentialkvotienten af en funktion f(x) således:

I differensregning arbejder man med differenser:

som er den "differentialkvotient" man kan få frem hvis x'erne er hele tal og h derfor mindst kan være 1. I differentialregning lærer man at man kan differentiere en potens efter formlen:

men uheldigvis gælder der ikke noget tilsvarende for differenser. Men - og det er det interessante - der findes en bestemt slags "potens" der opfører sig nogenlunde på samme måde som de kontinuerte potenser i differentialregning, nemlig størrelsen:

x^m = x(x-1)(x-2) ... (x-m+1)

altså et "faldende" produkt af m faktorer. x^m kaldes "x i m'te faldende". Der findes også en stigende potens, men den vil jeg ikke beskæftige mig med i dette essay. Lad os beregne D(x^m):

D(x^m) = (x+1)^m - x^m = (x+1)x(x-1)...(x-m+2) - x(x-1)(x-2)...(x-m+1)

= ((x+1) - (x-m+1))(x(x-1)(x-2)...(x-m+2) = mx^m-1

Der gælder altså en differensregel for faldende potenser, der er helt analog til differentiationsreglen for almindelige potenser.

Det interessante er nu at ligesom differentiation og integration er hinandens omvendte operationer i den kontinuerte matematik, så er differensdannelse og summation omvendte operationer i differensmatematikken. Der gælder nemlig følgende sætning:

g(x) = Df(x) hvis og kun hvis åg(x)dx = f(x) + Const

hvor summen er en uendelig sum med hensyn til x. Man kan i lighed med det kontinuerte tilfælde definere en "bestemt" sum, , og det gælder at:

Yderligere gælder der følgende sammenhæng mellem den almindelige sum fra forrige afsnit og denne nye "differenssum":

Altså: differenssummen er den samme som den ordinære sum hvor værdien i øvre grænse ikke medregnes.

Nu kan man så begynde at finde sammenhørende f'er og g'er, og det vil komme til at svare til en tabel over integraler, men blot med summer. Sådanne tabeller findes, og de letter summationsarbejdet betydeligt.

Det viser sig at det er hensigtsmæssigt at definere de faldende potenser også for nul og negative potenser. Defineres de således:

x⁰ = 1

får man egenskaber frem der er helt analoge til de ordinære potenser, men dog ikke helt identiske. Fx gælder det at

x^n+m = xⁿ(x-n)^m

altså næsten den sædvanlige potensregel. Differensreglen

Dxⁿ = nx^n-1

gælder derimod både for positive og negative værdier for n, og summationsreglen

gælder også, men dog ikke hvis n = -1. Det analoge tilfælde i integralregning fører som bekendt til den naturlige logaritme, men hvad med differensregning? Det vi søger er en funktion f(x) hvorom det gælder at

Det er ikke svært at se at funktionen

opfylder betingelsen. Denne funktion, som kaldes den harmoniske række, er altså den diskrete matematiks modstykke til den naturlige logaritme. Man har derfor

Den harmoniske række optræder atter og atter når man analyserer algoritmer. Værdien af H(n) er snævert forbundet med den naturlige logaritme, hvilket kan ses af at der ikke kan være så frygtelig stor forskel mellem en sum og et integral. Der gælder følgende tilnærmelse:

hvor g = 0.57721 56649... kaldes Eulers konstant. Udledelse og manipulation af sådanne asymptotiske formler er også en del af den konkrete matematik, som jeg imidlertid ikke vil komme yderligere ind på i dette essay.

Som bekendt er funktionen e^x uændret ved differentiation og integration. Findes der mon en tilsvarende "ufølsom" funktion indenfor differensregningen? Ja, det gør der, for det er let at se at

D(2ⁿ) = 2ⁿ⁺¹ - 2ⁿ = 2ⁿ(2-1) = 2ⁿ

så 2ⁿ er den diskrete matematiks eksponentialfunktion.

Lad mig som et eksempel på alt dette finde summen fra vores sorteringsproblem ved hjælp af differensteknikken. Det vi skulle finde var:

Nu er det let at se at k = k¹, så vi kan skrive:

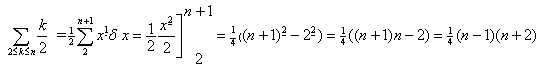
Med anvendelse af denne teknik bliver det et problem at omsætte "almindelige" udtryk til faldende potenser, men her er der også hjælp at hente i den konkrete matematik. Der gælder nemlig følgende formel:

hvor koefficienterne til x^k er Stirlingtallene af 2. art. Der findes en simpel algoritme der kan omsætte et vilkårligt polynomium til Sterling-form, som er en form hvor der i stedet for de almindelige potenser står faldende potenser. Hvis a'erne er det givne i nedenstående formel finder algoritmen b'erne:

a_nxⁿ + a_n-1x^n-1 + ... + a₁x + a₀ = b_nxⁿ + b_n-1x^n-1 + ... + b₁x¹ + b₀

b'erne kan da direkte indgå i en sum og blive "integreret".

Algoritmen udformes mest effektivt sådan at den ændrer koefficientarray'et a til at indeholde b'erne. Den ser da således ud:

for i := 1 to n-1 do begin

v := a[n];

for j := n-1 downto i do

a[j] := v := a[j] + i*v;

end;

Den er simpel, men subtil!

Det er herefter muligt at finde summen af et vilkårligt polynomieudtryk, næsten helt mekanisk. Fx finder vi, da k² = k² + k¹ ifølge ovenstående algoritme, at:

som stemmer med en af de mange magiske formler man finder i matematiske opslagsværker, og som lærebogsforfattere ofte blot postulerer og beviser ved hjælp af induktion.

Binomialkoefficienter

Størrelsen

der kaldes en binomialkoefficient, spiller en stor rolle ved analyse af algoritmer. Det kommer af at er det antal måder på hvilke man kan udvælge k elementer af en mængde på n elementer. Hvis man fx har en mængde på 4 elementer {a,b,c,d}, så kan man udvælge 2 elementer på måder, nemlig følgende:

{a,b} {a,c} {a,d} {b,c} {b,d} og {c,d}.

Regning med binomialkoefficienter er lidt af en kunst, og falder begynderen meget svært, men det er såmænd ikke så vanskeligt endda hvis man sætter sig lidt ind i det. Sagen er at binomialkoefficienterne har det ligesom de trigonometriske funktioner: der findes et gigantisk formelapparat som man må benytte sig af hvis man vil gøre sig indenfor den ædle binomialidræt.

Jeg kan ikke yde området retfærdighed i denne korte fremstilling, men vil nøjes med at anføre de vigtigste formler, heriblandt de formler jeg får brug for i de følgende datalogiske eksempler.

Man kan definere binomialkoefficienter for vilkårlige reelle værdier af r, specielt for r < 0, mens k skal være et helt tal. er pr. definition nul hvis k < 0 eller k > r; dette medfører at uendelige summer af binomialkoefficienter i realiteten bliver til endelige summer, og man behøver derfor ikke at være så streng med at holde rede på grænserne for en sum når man arbejder med binomialkoefficienter.

Den første regel for binomialkoefficienter er reglen om symmetri:

(1)

Den følger af at udvælgelse af k elementer er det samme som markering af de n-k elementer der ikke skal udvælges.

Den næste regel er reglen om at "sætte udenfor" eller "gange ind", absorbtionsreglen:

(2)

Den kan let vises ud fra definitionen. Så kommer den fundamentale additionsformel:

(3)

som følger af at hvis man fx maler et af de n elementer rødt, så må antallet af måder hvorpå man kan udvælge k elementer være lig med antallet med det røde element ekskluderet, , plus antallet med det røde element inkluderet, . Hvis man itererer lidt på denne additionsformel kan man udlede følgende to summationsformler:

(4)

og

(5)

Så findes der også en regel om at skifte fortegn på øverste indeks:

(6)

Denne regel er meget vigtig i forbindelse med omformning af binomialudtryk. Der er også formler for summer af produkter af binomialkoefficienter, hvor det indeks der summeres over befinder sig forskellige steder i de to faktorer. Jeg nævner de vigtigste; de gælder kun når alle indgående størrelser er hele tal

(7) (Vandermondes foldning)

(8) (h ³ 0)

(9) (h ³ 0)

(10) (h,m,n ³ 0)

(11) (h,m ³ 0; n ³ s ³ 0)

Arbejdet med binomialformler består i at overføre de formler man møder, til en af de former man finder i disse regler, hvorefter reglen kan anvendes. Lad os tage et eksempel.

Vi vil se på en algoritme der genererer alle undermængder, hvor n og k er givet. Uden tab af generalitet kan vi tænke os at de n elementer er de hele tal fra 1 til n incl. Man kan generere undermængderne i leksikografisk orden således:

1. Start med undermængden {1,2,...,k}.

2. Fjern det største element der endnu kan gøres større.

3. Erstat det fjernede element med et der er én større.

5. Lad alle efterfølgende elementer blive en stigende talrække, begyndende med erstatningselementet plus én.

Listen af undermængder for n = 5 og k = 3 i leksikografisk orden kommer da til at se således ud:

1 2 3

1 2 4

1 2 5

1 3 4

1 3 5

1 4 5

2 3 4

2 3 5

2 4 5

3 4 5

Ved at studere denne rækkefølge nøjere kan man komme frem til følgende algoritme:

for i := 1 to k do a[i] := i;

! Det var første subset;

while a[1] <> n-k+1 do begin

i := 1;

while a[k-i+1] = n-i+1 do i := i+1;

m := a[k-i+1];

for j := 1 to i do a[k-i+j] := m+j;

! Næste subset står nu i a;

end

Vi spørger nu om kompleksiteten af denne algoritme. Den ydre while-løkke gennemløbes gange, så kompleksiteten er mindst proportional med denne størrelse, hvilket jo er naturligt nok. Spørgsmålet er om man sætter noget til i den indre while-løkke. I denne løkke bestemmes i som det første indeks i a taget bagfra, hvorom det gælder at a[i] endnu ikke har fået sin maksimale værdi (som er n-i+1, se eksemplet). Hvor mange gange gennemløbes denne løkke pr. gennemløb af den ydre løkke?

Først må vi gøre os nogle kombinatoriske overvejelser. Løkken stopper når i har en værdi m, bestemt ved at a[k] = n, a[k-1] = n-1, ... , a[k-m+1] = n-m+1, men a[k-m] < n-m. På dette tidspunkt står der nogle tal i elementerne a[1] til a[k-m], som er sorteret i stigende orden, og hvori tallet n-m ikke kan forekomme (fordi det er det største af de tiloversblevne tal, og i så fald skulle have stået i a[k-m] pga. sorteringen). De tal der faktisk står i a[1] til a[k-m] må være en ud af de kombinationer af de n-m-1 øvrige "små" tal. Men det betyder at middelværdien af i bliver

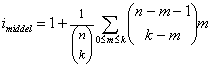
(1-tallet er der fordi løkken om man så må sige løber 1 for langt før det konstateres at den skal stoppe - man kan ikke vide om stopbetingelsen er opfyldt før man har afprøvet den.)

Det handler altså nu om at beregne summen

Det ser jo skræmmende ud, men lad os se på det. Den største vanskelighed er m'et der skal ganges ind i binomialkoefficienten, for der er ikke umiddelbart nogle af reglerne ovenfor der udtaler sig om denne situation. Kan man mon bruge absorbtionsreglen på en eller anden måde? Det nedre indeks, k-m, er i så fald uhensigtsmæssigt - der skulle have stået m. Jeg vil altså have der til at stå m i nedre indeks i stedet for k-m. Det kan jeg gøre ved at udskifte m med k-m:

=

Den første af disse summer kan findes ved at benytte (4) med r = n-k-1, og man finder:

Den anden sum er værre. Hvis vi sætter øvre og nedre indeks uden for, ved anvendelse af (2), forsvinder det famøse m ganske vist, men der kommer blot et andet i stedet for. Men vi kan fjerne det øvre m ved at bruge (6):

Nu kan vi bruge (2), og vi får herved:

Nu bruger vi (6) igen, blot den anden vej, og får:

Det næste skridt er at erstatte m med m+1:

og ved benyttelse af (4) med r = n-k finder vi endelig

Hele summen bliver derfor:

=

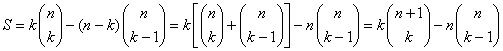
hvor jeg har benyttet (3) på knækparentesen. Nu kan vi endelig finde imiddel:

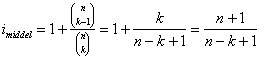
(omskriv de to binomialkoefficienter til fakultetsnotation og forkort). Vi ser at i_middel < 2 hvis k < (n+1)/2, og det kan man altid opnå ved anvendelse af symmetrireglen. Med andre ord: kompleksiteten er stadig proportional med - while-løkken skader ikke!

Frembringerfunktioner

Vi kommer nu til den del af den konkrete matematik der måske er den allervigtigste for datalogiske anvendelser, nemlig frembringerfunktionerne. Vi har set at man ofte kommer ud for at skulle manipulere med talfølger, der i princippet er uendelige, når man fx løser rekursionsligninger. Sådanne uendelige talfølger er meget upraktiske at arbejde med; det ville være lettere hvis man kunne repræsentere en uendelig talfølge ved hjælp af et "endeligt" udtryk. Frembringerfunktioner er netop sådanne afsluttede repræsentationer af (endelige og uendelige) talfølger.

Lad os antage at vi står overfor en talfølge:

T = {a₀,a₁,a₂,...,a_n,...}

Vi kan da "pakke talfølgen sammen" ved at skrive leddene op i en potensrække:

F(z) = a₀ + a₁z + a₂z² + ... + a_nzⁿ + ...

Det n'te led i talfølgen findes da som koefficient til zⁿ. Størrelsen z skal ikke opfattes som et tal, men som en indikator der skiller og nummererer de enkelte led i talfølgen; disse led svarer faktisk til cifrene i et tal med grundtal z. Man er ikke så meget interesseret i talværdien af udtrykket, men derimod i et afsluttet udtryk for summen, sådan rent formelt. Spørgsmålet om konvergens af den uendelige række er derfor ikke væsentligt; man forestiller sig ganske simpelt at z har en passende værdi. Fidusen er nu at hvis man kan beregne summen F(z), så har man et kompakt udtryk for hele talfølgen, og dette udtryk kan man manipulere med efter behov (fx differentiere eller integrere, lægge sammen eller gange med en anden frembringerfunktion etc.).

Ideen med frembringerfunktioner stammer vel oprindelig fra den kombinatoriske matematik, hvor man ifølge sagens natur arbejder meget med binomialkoefficienter. Opgaven at finde antallet af kombinationer af k ud af n elementer, hvor n er givet og k varierer, fører til talfølgen:

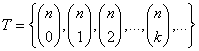
og frembringerfunktionen er:

men ifølge det velkendte binomialteorem:

er denne potensrække lig med:

Bemærk at hvis n er et positivt helt tal er summen i virkeligheden endelig, fordi binomialkoeffeicienterne til venstre for og til højre for er lig med nul. Hvis n er negativ eller reel fås en uendelig række, men formlen for F(z) gælder stadig. Denne formel spiller en stor rolle i hele teorien for frembringerfunktioner.

Men lad os se på et eksempel. Jeg begyndte med at fundere over kompleksiteten af sortering ved indsættelse, og kom frem til talfølgen:

Den hertil svarende frembringerfunktion må være:

Kan vi beregne denne sum? Ja, det kan man godt, men det er lidt uoverskueligt, så jeg vil hellere regne baglæns. Jeg påstår at

og vil vise at koefficienten til zⁿ er lig med . Til den ende udvikler jeg leddene i den krøllede parentes efter binomialformlen. Først det første led:

hvor jeg i sidste linie har skiftet fortegn for øvre indeks i binomialkoefficienerne, reguleret leddenes fortegn, og anvendt symmetrireglen for binomialkoefficienter, (1). På samme måde fås:

Denne regel er værd at huske; den udtrykker summen af en uendelig kvotientrække med kvotienten z:

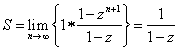
Nu kan vi finde koefficienten til zⁿ i udtrykket for F(z) (man ganger ind med z/2):

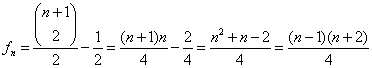
Fordelen ved denne metode er at den er helt rutinemæssig; man kan næsten lave et program der finder det n'te led ud fra en frembringerfunktion.

Men hvordan fandt jeg frem til frembringerfunktionen F(z)? Ja, det er en af de smarte ting ved hele teorien. Man kan nemlig finde en frembringerfunktion hvis man blot kender en rekursionsligning, og det gør vi jo. Jeg gentager den her for at have den for øje:

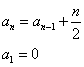
Én fremgangsmåde er følgende:

1) Reducer rekursionen til én enkelt ligning, der gælder for alle n.

Det gælder altså om at samle de to udtryk for a i ét. Vi kan selv bestemme hvad a skal være til venstre for n = 1, og vælger arbitrært a₀ = a_-1 = a_-2 = ... = 0. Men så bliver a₁ = 1/2 efter første ligning, hvilket er 1/2 for meget. Første ligning må med andre ord modificeres for at få det hele til at stemme. Hvis det havde været C++ eller Java var det let klaret:

a[n] = a[n-1] + n/2 - (n == 1? 1/2 : 0);

Vi mangler en "matematisk" notation der giver udtryk for det samme. I den konkrete matematik har man adopteret en notation der skyldes Kenneth Iverson, der i sin tid indførte den i programmeringssproget APL. Den går ud på at man kan skrive et logisk prædikat i knækparentes, fx [n lige]. Værdien af et sådant udtryk skal være 1 hvis prædikatet er true og ellers 0. Nu kan første rekursionsligning skrives:

Det var første skridt.

2) Multiplicer ligningen med zⁿ og summér over alle værdier af n (dvs. fra minus uendelig til uendelig).

Vi får da:

3) Find frembringerfunktionen F(z) = åa_nzⁿ ud fra den fundne ligning

Vi ser at venstre side af ligningen er lig med F(z). Første led på højre side kan skrives:

da summen går over alle n. Det sidste led giver kun noget når n = 1, dvs. z/2. Heraf fås:

For at finde F(z) må vi nu beregne summen ånzⁿ. Det simpleste er at slå op i en tabel. Sådan én findes fx i Graham(1989). Her finder vi følgende:

talfølge	frembringerfunktion	sluttet form
1, 2, 3, 4, 5, 6, ...

som er næsten det rigtige. Hvis vi ganger med et ekstra z får vi den ønskede funktion frem. Den sluttede form for leddet bliver derfor:

Man kan selvfølgelig også give sig i kast med at finde summen "the hard way". I dette tilfælde kan man benytte et trick som hyppigt kommer på tale i praksis, nemlig at under meget generelle betingelser, som næsten altid vil være opfyldt i praksis, vil integralet af en sum være lig med summen af integralet. Vi skriver:

ånzⁿ = zånz^n-1

Ved integration af leddene under summationstegnet fås:

Denne sum er den uendelige kvotientrække fra før med summen:

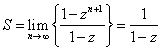
Den oprindelige sum fås herefter ved differentiation:

som ved multiplikation med den manglende faktor giver samme resultat som vi kunne slå op i tabellen. Endelig kan vi så opskrive frembringerligningen:

og vi finder:

i overensstemmelse med hvad jeg påstod ovenfor.

Relevansen af alt dette her er, at vi kan se en generel metode til løsning af rekursionsligninger tone frem. Hvis jeg var begyndt med rekursionsligningen og havde fundet frembringerfunktionen, og derefter havde udviklet den i en potensrække, ville jeg være kommet frem til løsningen. Det eneste ikke-rutineprægede skridt i hele processen består i at finde summen ånzⁿ, og den kunne man endda slå op i en tabel.

Sandsynligheder

Sandsynlighedsovervejelser spiller en stor rolle når man analyserer algoritmer. Vi har allerede set et eksempel i analysen af sortering ved indsættelse, hvor leddet n/2, der repræsenterer arbejdsmængden ved at indsætte et nyt element i en sorteret følge af n elementer, er resultatet af en sandsynlighedsovervejelse.

Den sandsynlighedsregning der er aktuel i forbindelse med algoritmeanalyse er altid af den slags, hvor det drejer sig om at bestemme sandsynligheden for visse diskrete hændelser. Her er det sådan at man har en vis mængde af elementære hændelser der udgør et sandsynlighedsrum, det univers man arbejder indenfor, og til hver hændelse er der knyttet en vis sandsynlighed, som er et reelt tal mellem 0 og 1 incl. Summen af sandsynlighederne i et givet sandsynlighedsrum er altid 1.

Kast med en terning er et godt eksempel. Der er 6 elementære hændelser, og hvis terningen ikke er en snydeterning har alle hændelser den samme sandsynlighed 1/6. Rigtige terninger vil altid være mere eller mindre skæve, så denne sandsynlighedsfordeling er en abstraktion, men det ser man ofte bort fra i sandsynlighedsberegninger.

Sandsynlighedsberegninger drejer sig nu bl.a. om at finde sandsynligheder for sammensatte hændelser, fx sandsynligheden for at få 12 øjne ved to kast med én terning, eller ved ét kast med to terninger. Det er ikke på forhånd givet at disse to sammensatte hændelser har den samme sandsynlighed, men det har de tilfældigvis fordi de to elementære hændelser ved to kast med én terning er indbyrdes uafhængige. Så kan man nemlig bruge den første grundregel for sandsynlighedsregning: sandsynligheden for "både og" er lig med produktet af sandsynlighederne, og vi finder:

S(tolv) = S(seks)*S(seks) = 1/6*1/6 = 1/36

Hvis man kaster med to terninger er der 6 muligheder for den ene terning og for hver af dem 6 muligheder for den anden terning, altså i alt 6*6 = 36 udfald; kun ét udfald giver 12 øjne, og sandsynligheden bliver igen 1/36.

Denne sandsynlighed fortæller også noget andet, nemlig at hvis man kaster to terninger mange gange efter hinanden, så vil de vise to seksere ca. hver 36. gang. Der vil være en vis afvigelse i denne regelmæssighed, og det kunne være af interesse at vide hvor stor denne afvigelse er. Den slags spørgsmål giver sandsynlighedsregningen svar på.

Nu skal dette essay ikke være et kursus i sandsynlighedsregning, og jeg vil derfor indskrænke mig til en kort omtale af de vigtigste regneregler og definitioner. Lad a og b være to hændelser med sandsynligheder p(a) og p(b). Da er:

p(a and b) = p(a)p(b)

hvis hændelserne er indbyrdes uafhængige. Endvidere gælder generelt:

p(a or b) = p(a) + p(b) - p(a and b)

som reduceres til

p(a or b) = p(a) + p(b)

hvis hændelserne udelukker hinanden.

Et vigtigt begreb i hele teorien er en stokastisk variabel. Herved forstås en størrelse der ved forskellige iagttagelser af samme kategori af hændelser kan antage forskellige værdier. Øjeantallet ved kast med en terning er en stokastisk variabel, og antallet af sammenligninger for en sorteringsalgoritme er en stokastisk variabel. Ved middelværdien af en stokastisk variabel X, der kan antage værdierne i mængden M = {x₁,x₂,x₃,...,x_n} forstås summen:

E(X) står for "expected value of X", og er den værdi af X man vil få frem "i snit" ved mange eksperimenter. Der gælder følgende simple regler for middelværdier:

E(X + Y) = E(X) + E(Y)

hvor X og Y er stokastiske variable for samme sandsynlighedsrum. Hvis k er en konstant gælder endvidere:

E(kX) = kE(X)

Multiplikationsreglen er mere indviklet, men hvis X og Y er indbyrdes uafhængige gælder den simple regel:

E(XY) = E(X)E(Y)

Afvigelser fra middelværdien måles ved hjælp af variansen:

V(X) = E((X - E(X))²)

På grund af potensopløftningen bliver varianserne ofte store tal, så det er almindeligt at man i stedet regner med spredningen:

Hvis X er en stokastisk variabel der kun antager positive værdier, kan man bekvemt sammenfatte en hel sandsynlighedsfordeling ved hjælp af en frembringerfunktion:

En sådan frembringerfunktion indeholder al information om X. Alle koefficienter er positive sandsynligheder, og deres sum er lig med 1. Middelværdien af X kan beregnes ud fra frembringerfunktionen ved at differentiere mht. z og derefter sætte z = 1:

På tilsvarende måde kan man vise at variansen er

Lad os afprøve disse ideer på et simpelt eksempel. Hvor længe skal man i gennemsnit slå med en terning for at få en sekser?

Lad sandsynligheden for at få 6 være p, og sandsynligheden for at få noget andet være q = 1-p. Frembringerfunktionen for den stokastiske variable X = "antal kast indtil første sekser" bliver da:

Heraf finder vi:

og:

Ved indsættelse af p = 1/6 fås:

E(X) = 6

V(X) = 30

At middelværdien var 6 ville man jo nok have gættet på, men vi ser at denne middelværdi har en stor spredning, nemlig = ca. 5.5, hvilket ikke er særligt indlysende.

Med de redskaber til rådighed som jeg har gennemgået i dette essay, er det muligt at løse ganske vanskelige kompleksitetsproblemer. Jeg vil vise et eksempel der handler om en særlig datastruktur der er velegnet til repræsentation af en prioritetskø.

Datastrukturen hedder et p-træ. Et p-træ er et binært træ der kan være tomt. Venstregrenene i forhold til en rod danner en ordnet følge af knuder i stigende prioritetsorden, den såkaldte venstresti. Til hver knude i venstrestien (med undtagelse af den sidste) er der knyttet et p-træ, det såkaldte højretræ. Alle knuderne i det højretræ der er knyttet til knuden x i venstrestien, har prioriteter der ligger mellem prioriteten af x og prioriteten af x's efterfølger i venstrestien, se fig. 1.

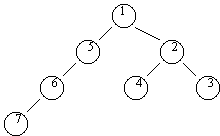
Fig. 1. Et p-træ med 7 knuder, der er indsat i rækkefølgen 6, 5, 7, 1, 2, 4, 3.

Indsættelse af en ny knude i et p-træ kan ske som vist i nedenstående objektorienterede algoritme, programmeret i C++. Der er to slags objekter: selve træet og knuderne. Træet peger på en "spøgelsesknude" ved hjælp af attributten root; denne uegentlige første knude er der for at undgå at roden i det egentlige p-træ kommer til at indtage en særstilling der ville komplicere algoritmerne. Hver knude har en nøgle (key), der er prioriteten for knuden, samt to referencer, left og right, der peger på hhv. efterfølgeren i venstrestien, og højretræet. Af hensyn til algoritmen har hver knude også en attribut der peger på dens far (father). Det er let at se ud fra algoritmen at det element, der har den laveste prioritet, vil stå forrest i venstestien, mens det element, der har den højeste prioritet, vil stå sidst i venstrestien.

Problemet er nu at beregne det gennemsnitlige antal sammenligninger for at indsætte et nyt element i et p-træ. En sådan undersøgelse kan deles i to dele, nemlig svarende til indsættelse i venstrestien og svarende til indsættelse i højretræet. Jeg vil her nøjes med at se på indsættelse i venstrestien.

struct Pnode

{

Pnode *left,*right,*father;

int key;

Pnode(int k)

{

left = right = father = 0;

key = k;

}

void insert(Pnode* x);

void traverse(int n);

};

struct Ptree

{

Pnode *root;

//Roden har en nøgle der er mindre end alle andre nøgler

Ptree()

{ root = new Pnode(-1); }

void insert(int k);

void traverse();

};

void Ptree::insert(int k)

{

Pnode *node = new Pnode(k);

//Hvis der allerede er et træ, indsætter vi i det

if (root->left) (root->left)->insert(node);

//og ellers danner vi et.

else root->insert(node);

}

void Pnode::insert(Pnode* x)

{

if (key > x->key) //Vi har nået indsætningspunktet

{

//Det er enten en venstre- eller en højregren

//x indsættes foran this

if (father->left == this) father->left = x;

else father->right = x;

x->left = this; x->father = father; father = x;

return;

}

if (!left) //Har vi nået enden af en venstregren?

{

left = x; x->father = this;

return;

}

//Her kommer skanning af en venstregren

if (left->key < x->key) { left->insert(x); return; }

//Her går vi ind i et højretræ

if (right) { right->insert(x); return; }

//Højretræet var tomt

right = x; x->father = this;

return;

}

Som det kan ses af algoritmen er indsættelse i venstrestien faktisk en (rekursiv) lineær søgning ned gennem left-pointerne, og det kan derfor være interessant at finde ud af hvor lang venstrestien bliver i gennemsnit. Det er klart at hvis n knuder indsættes i nummerorden, så vil venstrestien have længden n, og indsættelse af hver knude sker bagest i venstrestien; det er ikke særlig hensigtsmæssigt. Strukturen er altså kun egnet hvis nøglerne ankommer i mere eller mindre tilfældig orden.

Med baggrund i ovenstående betragtninger opstiller jeg nu en sandsynlighedsmodel, der skal repræsentere den tilfældige ankomst af knuder til træet. For det første tænker jeg mig, at det er de lige tal fra 2 til 2n der er prioriteter, og at der ikke er gengangere blandt tallene. Endvidere tænker jeg mig at alle permutationer af disse tal er lige sandsynlige; en bestemt permutation har altså sandsynligheden.

Hvis man prøver at opbygge p-træer svarende til alle n! mulige rækkefølger af indsættelser får man en mængde af p-træer, T, men der vil være færre end n! p-træer i T, da der er mange rækkefølger der fører til samme p-træ.

Den gennemsnitlige effektivitet af algoritmen kan nu måles ved at beregne antallet af sammenligninger der bliver udført for at indsætte et tilfældigt udvalgt element fra mængden

M = {1,3,5,...,2n+1}

Altså de ulige tal, i et tilfældigt udvalgt træ fra mænden T. Bemærk at der ikke er nogle sammenfald af værdier mellem M og elementerne i T.

Elementerne i M vælges helt tilfældigt, så hvert element har samme sandsynlighed, , for at blive valgt. Lad nu p_n,k være sandsynligheden i T for et p-træ med n knuder og en venstresti af længde k. Når man indsætter det valgte element fra M i sådan et p-træ, bliver venstrestien 1 større hvis det valgte element var enten 1 eller 2n+1 (sandsynlighed ), mens den er uændret i alle andre tilfælde (sandsynlighed). Træet vil dog under alle omstændigheder indeholde n+1 elementer efter indsættelsen. Man kan derfor opstille følgende rekursion for p_n,k:

Startbetingelsen følger af, at et p-træ med 2 knuder altid har en venstresti på 2, og ingen højretræer. P-træer med færre end 2 knuder ser jeg bort fra - de er uinteressante og forplumrer blot beregningerne. Nu indfører jeg frembringerfunktionen:

og ved summation og omordning af leddene i rekursionsligningen fås:

Nu er

Her er sandsynligheden for at et p-træ med n elementer har en venstresti på 1; men den er nul ifølge forudsætningerne. p_n,n er sandsynligheden for at venstrestien er n lang i et p-træ med n knuder, dvs. at prioriteterne er indsat i stigende eller faldende rækkefølge. Denne sandsynlighed bliver meget lille, , når n vokser, så vi kan uden de store fejl se bort fra leddet p_n,nzⁿ, så meget mere som det skal trækkes fra og derfor bidrager til at forbedre det endelige resultat. Ved at se bort fra leddet får vi en løsning der er lidt dårligere end den virkelige, men hvis denne tilnærmede løsning er god nok er alt jo i orden. Vi finder derfor:

(n+1)G_n+1(z) = (n-1)G_n(z) + 2zG_n(z)

G₂(z) = z²

Dette er en rekursion udfra hvilken G_n(z) kan findes, men det er ikke nødvendigt i vores tilfælde. Vi ved at G_n'(1) er middelværdien af k, dvs. middelværdien af venstrestiens længde, så vi kan blot differentiere rekursionsligningen og sætte z = 1. Dette fører til:

(n+1)G_n+1'(z) = (n-1)G_n'(z) + 2G_n(z) + 2zG_n'(z)

Nu er

da summen er over samtlige muligheder for k (p_n,1 er nul). Derfor får vi:

(n+1)L_n+1 = (n-1)L_n + 2 + 2L_n

hvor L_n er middellængden af venstrestien i et p-træ med n knuder. Ved omordning af leddene fås:

L₂ = 2

hvor startbetingelsen stammer fra differentiation af G₂(z). Denne rekursion er af den simple type vi tidligere har stiftet bekendtskab med. Den kan skrives på formen:

L₂ = 2

og løsningen er:

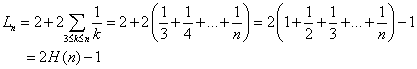
Vi ser at venstrestien (og dermed søgningen i venstrestien) kun vokser logaritmisk med n.

Nu kan man gå videre og se på søgningen i højretræerne. Det er noget vanskeligere, men kan gennemføres med de teknikker jeg har omtalt. Jeg henviser den interesserede læser til Jonassen(1975).

Multipel indsættelse

Sortering ved indsættelse, som var det første eksempel i dette essay om konkret matamatik, kan generaliseres som først beskrevet af Isaac & Singleton, se Isaac(1956). Ideen er at arbejde med m grupper der hver for sig sorteres ved indsættelse. De n elementer, x(1..n), der skal sorteres, fordeles på de m grupper ved hjælp af en fordelingsfunktion, f(x), der beregner et gruppenummer ud fra argumentet x. Funktionen f(x) skal være monotont voksende, således at den skiller elementerne i disjunkte klasser. Idet insertion(x) er den algoritme der er angivet i begyndelsen af dette essay, og tænkes at være en metode i klassen gruppe, kan algoritmen beskrives således i et Pascal-lignende pseudosprog:

for k := 1 to m do L[k] := new gruppe;

for i := 1 to n do begin

k := f(x(i)); L[k].insertion(x(i))

end;

// Nu står de sorterede elementer i L[1] til L[m]

sat i forlængelse af hinanden;

Det er klart at kompleksiteten af denne algoritme er mindst O(n) på grund af i-løkken. Spørgsmålet er hvor galt det går når insertion kaldes inden i denne løkke. Som vi fandt frem til i starten er kompleksiteten af insertion O(l²) hvis der er l elementer at sortere. Lad os derfor finde middelværdien af l², hvor l er middellængden af en gruppe.

Vi ser derfor nu på én af de m grupper, med det formål at finde frembringerfunktionen G(z) for længden l af denne gruppe. Hvis alle permutationer af elementer i x-array'et er lige sandsynlige, har ethvert element sandsynligheden for at ende i den betragtede gruppe og sandsynligheden for at havne i en af de andre grupper. Frembringerfunktionen for ét x kan derfor udtrykkes som . Da der er n indbyrdes uafhængige x'er i alt bliver frembringerfunktionen for hele processen:

Opgaven består nu i at beregne E(l²) ud fra G(z). Vi har tidligere set at E(l) = G'(1) og V(l) = G''(1) + G'(1) - G'(1)². Nu gælder det imidlertid at variansen

V(l) = E((l - E(l))²) = E(l² - 2lE(l) + E(l)²)

= E(l²) - 2E(l)E(E(l)) + E(E(l)²)= E(l²) - 2E(l)E(l) + E(l)²

= E(l²) - E(l)²

hvor jeg har benyttet at E(l) er en konstant, og at det derfor må gælde at E(E(l)) = E(l), og analogt for E(l)². Men dette viser at:

E(l²) = V(l) + E(l)² = G''(1) + G'(1) - G'(1)² + G'(1)²

= G''(1) + G'(1)

Differentiation af frembringerfunktionen giver nu:

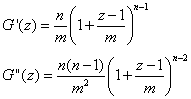
og vi finder sluttelig:

Denne formel er et udtryk for middelværdien af tiden for sortering af en gruppe. Størrelsen er det gennemsnitlige antal elementer pr. gruppe. Vi kender ikke spredningen på denne størrelse, den afhænger af datamaterialet, men forudsætningen for metoden var, at vi kendte vores data så godt, at vi kunne vælge en funktion f(x), der skiller dataene i m grupper, der er omtrent lige store. Hvis denne forudsætning holder stik, er tilnærmelsesvis konstant, og vi kan skrive:

E(l²) = ca. c(1+c) = O(1)

Vi har hermed vist at man med denne metode kan sortere n elementer i en tid der er proportional med n, mod sædvanligvis nlog(n). Hvis man ikke har en god funktion, der adskiller dataene effektivt, er metoden farlig. Hvis alle elementer falder indenfor samme gruppe bliver sorteringstiden O(n²), så metoden er meget følsom overfor skævheder. Man ser også at c skal være så lille som muligt, dvs. så stort m som muligt. Den hurtigste proces fås for c = 1, dvs. m = n, hvilket stemmer med, hvad man ville forvente (der bliver ét element i hver gruppe, og sortering af ét element tager ingen tid).

Quicksort

En af de mest berømte algoritmer i nyere datalogi er den sorteringsalgoritme der går under navnet quicksort (Hoare(1962)). De fleste lærebøger i datalogi omtaler denne metode, og der er også mange der gør et forsøg på at analysere den. Det er imidlertid min erfaring, at disse analyser ofte ikke er helt nøjagtige, selv om hovedresultatet - nemlig at quicksort har kompleksiteten O(nlog(n)) - jo uvægerligt nås. Lad mig slutte dette essay med en analyse af quicksort hvor jeg tager udgangspunkt i en konkret realisering af algoritmen, og hvor jeg forsøger på ikke at gøre nogle tilnærmelser undervejs i analysen. Da quicksort bygger på ombytning af elementer, og ombytning er en kostbar proces i en sekventiel maskine, vil jeg både finde gennemsnit for sammenligninger og ombytninger.

Algoritmen, der ses nedenfor, sorterer de elementer der befinder sig i array a mellem indeksværdier low og high incl. i stigende orden. Først findes deleværdien v som det midterste tal i den mængde, der skal sorteres. Man kan også blot tage det første tal eller et tilfældigt af tallene. Hvad man skal gøre er blevet diskuteret meget i tidens løb, men det synes som om Sedgewick har fundet de vises sten når han i Sedgewick(1978) foreslår at vælge medianen af de tre første tal. Men jeg vælger altså det midterste tal som deleværdi. Valget spiller ingen rolle for den overordnede kompleksitet af algoritmen, kun for finjustering til maksimal ydelse.

procedure quicksort(var a: array; low,high: integer);

var i,j,v,t: integer;

begin

i := low; j := high;

v := a[(i+j) div 2];

while i < j do

begin

while a[i] < v do i := i+1;

while v < a[j] do j := j-1;

if i <= j then begin

t := a[i]; a[i] := a[j]; a[j] := t;

i := i+1; j := j-1

end

end;

if low < j then quicksort(a,low,j);

if i < high then quicksort(a,i,high)

end ;

De to pegepinde, i og j, bevæges nu ind imod hinanden indtil man finder to elementer, a[i] og a[j], der står "forkert" i forhold til deleværdien; a[i] er større end eller lig med deleværdien og a[j] er mindre end eller lig med deleværdien. Da selve deleværdien jo befinder sig midt i den mængde der skal sorteres, vil denne betingelse altid blive opfyldt på et eller andet tidspunkt, og det er bl.a. denne egenskab der er med til at gøre algoritmen hurtig (man behøver ingen ekstra test på om i og j krydser hinanden i de inderste while-løkker, de er så "minimale" som vel tænkes kan).

Nu kommer så undersøgelsen af om de to fundne elementer skal ombyttes; det skal de hvis i ligger til venstre for j, altså hvis der ikke er krydsning af pegepindene. I algoritmen testes der på om i <= j, men hvis i = j sker der en ombytning af et element med sig selv - en ubehagelig ineffektivitet! Grunden er at jeg skal have ændret værdierne af i og j også i dette tilfælde, sådan at der konstateres en krydsning i den ydre while-løkke. Det kan naturligvis effektiviseres, men det spiller heller ingen rolle for selve analysen.

Når en krydsning af i og j er konstateret vil hele datamængden være opdelt på en sådan måde, at alle de elementer der ligger til venstre for j er mindre end v, og alle de elementer der ligger til højre for i er større end v. Disse delmængder kan nu sorteres hver for sig ved hjælp af quicksort.

Nu til selve analysen. Først antallet af sammenligninger. Først opstiller jeg en sandsynlighedsmodel; den er den samme som jeg brugte i forbindelse med p-træerne: det er tallene fra 1 til n der skal sorteres, og alle startpermutationer er lige sandsynlige.

Antallet af sammenligninger for at sortere n elementer kalder jeg a_n. Det kræver n-1 sammenligninger at få i og j til at krydse hinanden, og når det sker er datamængden delt i to. Lad k være indeks for delepunktet; der er da k-1 elementer i den ene del og n-k elementer i den anden (k-1+n-k = n-1, og selve deleværdien går fra). Sortering af disse delmængder kræver hhv. a_k-1 og a_n-k sammenligninger. Da enhver værdi af k har samme sandsynlighed, nemlig 1/n, kan middelværdien af antallet af sammenligninger beregnes ved at finde gennemsnittet taget over k-værdierne, således:

Dette er den første ligning i en rekursion for kompleksiteten af quicksort. Det ser jo frygtindgydende ud, men det viser sig at man let kan reducere ligningen til noget kendt - eller i hvert fald omtrent til noget vi har set før. Jeg tager først fat på det sidste led og bruger (bl.a.) den kommutative lov for summation:

Herved er sidste led i rekursionsligningen omdannet til at være af samme form som næstsidste led, og vi kan skrive:

Det skabte en smule luft, men stadig er der et n i nævneren på en brøk, samt - værst af alt - den alarmerende sum. n'et er hurtigt klaret:

Summen kan vi slippe af med ved hjælp af et trick. Vi opskriver rekursionen for et n der er 1 mindre:

og så trækker vi de to ligninger fra hinanden:

na_n - (n-1)a_n-1 = n(n-1) - (n-1)(n-2) + 2a_n-1

idet alle led i summerne med undtagelse af det sidste i den øverste ligning ophæver hinanden. Ved ordning af leddene i denne nye ligning fås:

na_n = (n+1)a_n-1 + 2(n-1)

Pyha! Nu kan vi ånde lettet op; det begynder at ligne noget vi kender. Det er bare ærgerligt at koefficienterne til a_n og a_n-1 er forskellige. Kan vi mon ikke få dem gjort ens? Det vi gerne vil er at kunne skrive noget i retning af a_n = a_n-1 + f(n), for det er den type ligninger vi kender. Vi prøver derfor at multiplicere på begge sider af lighedstegnet med en eller anden funktion af n, s_n:

ns_na_n = (n+1)s_na_n-1 + 2s_n(n-1)

Det gælder nu om at finde s_n således at leddet (n+1)s_n kan omdannes til (n-1)s_n-1, for så kan man, ved at foretage substitutionen b_n = ns_na_n, få omdannet ligningen til den simple form vi kender. Derfor kræver vi at (n+1)s_n = (n-1)s_n-1, dvs.

Denne rekursion kan man nu iterere, og man finder:

Med denne værdi af s_n omdannes ligningen til:

eller:

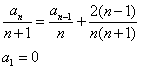
hvor jeg har tilføjet en passende startbetingelse, der passer med min algoritme (low = high i yderste inkarnation).

Denne metode til at transformere en rekursion over i noget simplere er helt generel. Faktoren s_n kaldes en summationsfaktor, og brugen af summationsfaktorer kan ofte hjælpe én med at løse stygge rekursioner. I mange artikler og lærebøger bliver summationsfaktorerne nærmest trukket op af en høj hat, som en slags tryllekunst, men som man ser er der ikke tale om magi; summationsfaktorer kan findes helt mekanisk.

Variabelsubstitutionen fører rekursionen over i:

der har løsningen:

Summen kan deles i to ved at dividere op i hvert led i k-1:

Lad os tage disse summer én ad gangen.

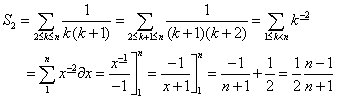
Løsningen til b-rekursionen er derfor:

og da a_n = (n+1)b_n fås endelig:

a_n = 2(n+1)H(n+1) - 2(2n+1)

Det var en ret kompliceret beregning, og kan man nu være sikker på at der ikke er begået nogle regnefejl undervejs? Det kan let undersøges ved at iterere sig frem i den oprindelige rekursion for små værdier af n, og sammenligne med den værdi man får ved at sætte ind i den sluttede form. Jeg har gjort det for de første fire værdier af n, og fandt: a₁ = 0, a₂ = 1, a₃ = og a₄ = ud fra begge formler. Prøv selv; det er fascinerende at se hvordan helt forskellige mellemregninger i de to formler på magisk vis fører til samme slutresultat.

Da H(n) har kompleksiteten O(log(n)) ser vi at quicksort har kompleksiteten O(nlog(n)), som det hævdes af alle autoritative kilder. Man kunne måske nok komme frem til et omtrentligt resultat på en nemmere måde, men nu er vi i hvert fald sikre på vores bedømmelse.

Men nu til antallet af ombytninger, b_n. Hvis sandsynligheden for, at delepunktet kommer til at ligge ved indeks k, og der da er udført netop t ombytninger, kaldes p_k,t, så må man i analogi med sammenligningstilfældet kunne skrive:

Ligningen er blot en dannelse af middelværdien af den stokastiske variable "antal ombytninger", efter den sædvanlige formel: sandsynlighed gange antal. Vanskeligheden er at der nu er et t der varierer, mens vi før blot havde et konstant antal sammenligninger, nemlig n-1.

Der er nok ingen vej uden om: vi må finde p_k,t, og det er det svære i denne opgave, mens resten er mere eller mindre rutinearbejde for en konkret matematiker. Lad os derfor gå i krig med p_k,t.

Da der er n! lige sandsynlige talmængder som inddata til algoritmen, må p_k,t være lig med det samlede antal muligheder for ombytningsmønstre, divideret med n!. Størrelserne k og t skal opfattes som kendte og faste størrelser, og vi skal finde det samlede antal mulige ombytninger for netop disse værdier af k og t.

Jeg minder om sandsynlighedsmodellen, som arbejder med den forudsætning at det er en permutation af tallene fra 1 til n der skal sorteres. Hvis der opdeles sådan at position k bliver delepositionen, så betyder det altså at tallet i position k netop er lig med k, og tallene til venstre er en permutation af tallene fra 1 til k-1, mens tallene til højre er en permutation af tallene fra k+1 til n. Før opdelingen var der præcis t af tallene i den venstre gruppe, der skulle have stået i den højre - og omvendt. Disse overvejelser giver nøglen til beregning af p_k,t.

De to delmængder kan permuteres på hhv. (k-1)! og (n-k)! måder, så det samlede antal permutationer for de to dele taget som et hele er (k-1)!(n-k)!. For hver af disse permutationer skal der udtages t ombytningspositioner i hver delmængde. Det kan gøres på måder. Man har derfor at

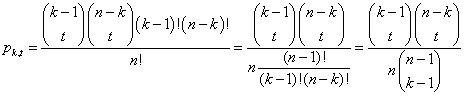
Så kom vi så langt, men nu venter der os sandelig nogle barske binomialsummationer, når vi indsætter i rekursionen. Lad os først dele højresiden af rekursionen i to summer:

Summerne er i virkeligheden dobbeltsummer fordi der skal summeres over både k og t. Summen over k går fra 1 til n og summen over t går fra 0 til k-1. Det er derfor det fornuftigste at summere over t "inden i" k. Lad os tage hver sum for sig og begynde med den sidste sum; den ser lettest ud fordi der ikke er noget t uden for binomialkoefficienterne. Vi finder:

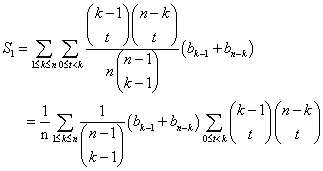
Summen over t kan nu beregnes ved at benytte sumformlen (8) hvori man substituerer h = k-1, s = n-k, k = t og m = n = 0. Dette giver:

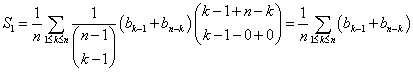
Hele den imposante sum blev altså reduceret til, hvilket man måske kunne have gættet ud fra erfaringerne med rekursionen for antal sammenligninger. Tilbage er den anden sum i ombytningsrekursionen:

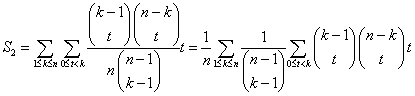
Her benytter jeg binomialregel (2) på og får:

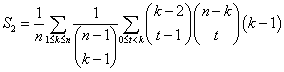
Faktoren (k-1) afhænger ikke af t og kan sættes udenfor t-summen, og så kan man benytte sumformel (8) igen, men nu med substitutionerne h = k-2, s = n-k, m = -1 og n = 0. Dette fører til:

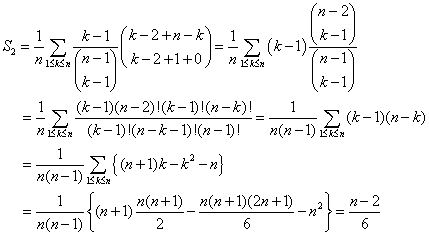
Hele rekursionen kan herefter skrives:

Denne rekursion kan løses på præcis samme måde som rekursionen for antal sammenligninger; løsningen fandt jeg til:

Sammenligner vi nu dette resultat med resultatet for antal sammenligninger ser vi, at der udføres ca. 6 gange så mange sammenligninger som ombytninger i quicksort. Det lave antal ombytninger er også en af grundene til at quicksort lever op til sit navn. Da en sammenligning kræver 2 lagertilgange, og en ombytning på en sekventiel maskine kræver 6 lagertilgange (se procedure quicksort) kan vi slutte at der i gennemsnit bruges halvt så megen tid på ombytninger som på sammenligninger i quicksort.

Opsummering

I dette essay førte jeg læseren hastigt igennem de mest fundamentale sider af den konkrete matematik. I sin fulde almindelighed er den konkrete matematik mere omfattende end det fremgår af dette essay, der er tale om matematik og ikke blot dens anvendelse på datalogiske problemer. De vigtigste emner jeg har udeladt er hele talteorien, samt spørgsmålet om hvordan man udvikler og regner med asymptotiske udtryk (O-notation). Det er ikke fordi disse emner er uden interesse for datalogen, men fordi dette blot er et essay, dvs. en kort afhandling af populært tilsnit.

Jeg begyndte med at omtale rekursionsligninger og deres løsning, og dette emne blev gradvist uddybet hen igennem essayet. Der er meget mere at sige om løsning af rekursioner, og jeg kan henvise den interesserede læser til Lueker(1980). Opstilling af en rekursion er ofte det første skridt i arbejdet med at beregne kompleksiteten af en given algoritme, og jeg håber at have givet læseren en fornemmelse af at hvis det først er lykkedes at opstille en rekursion, så er resten blot mere eller mindre rutine. Desværre kender jeg ingen opskrift på denne første fase, at opstille selve rekursionen, det er her den kreative indsats ligger.

Løsning af rekursioner involverer næsten altid en eller anden form for summation, og derfor handlede næste afsnit om summation. Jeg nævnte de fundamentale regler for summation og viste nogle eksempler på sumdannelse ved anvendelse af disse regler. Også dette emne blev uddybet hen igennem essayet.

Den første uddybning handlede om analogien mellem differentiation og differensdannelse, altså en analogi imellem den kontinuerte og den diskrete matematik. Her viste jeg hvordan man kan indføre et sumbegreb der svarer til den kontinuerte matematiks integrationsbegreb. Jeg indskrænkede mig til at se på potenser fordi det har størst anvendelse indenfor algoritmeanalyse, men differensregning har, som matematisk disciplin betragtet, langt større omfang; fx er differensregning en vigtig del af hele den numeriske matematik, regning med datalogiens repræsentationer af reelle tal.

Så fulgte et afsnit om binomialkoefficienter, måske det matematiske objekt der er mest fremmedartet for den der er opdraget i den kontinuerte matematiks verden. Jeg viste et eksempel på en rigtig "ond" summation med binomialkoefficienter, og håber at have givet læseren en fornemmelse af at vi her står overfor et område der minder lidt om trigonometri i den forstand at det handler om at kende sit formelapparat når man skal manipulere med binomialkoefficienter.

Tanken om at konstruere frembringerfunktioner bør ikke være fremmed for en datalog. En frembringerfunktion er en repræsentation af en talfølge, der gør det muligt at behandle hele talfølger, endelige og uendelig, under ét i en afsluttet form. Jeg viste ved et eksempel hvordan man kan benytte dette vigtige redskab til løsning af rekursioner.

Efter en kort omtale af det diskrete sandsynlighedsbegreb introducerede jeg frembringerfunktioner for sandsynligheder, og viste hvordan man kan bruge sådanne til analyse af algoritmer. Eksemplerne var dels en datastruktur til administration af prioritetskøer, og dels en sorteringsmetode der under visse omstændigheder er i stand til at sprænge "sorteringsmuren" nlog(n).

Mit essay sluttede med en ret indgående analyse af en af de mest omtalte algoritmer i moderne datalogi, nemlig quicksort, hvor jeg både behandlede antallet af sammenligninger og antallet af ombytninger. Her fik jeg brug for det meste af det stof der var blevet omtalt tidlige i essayet.

Referencer

[Graham (1989)]

Ronald L. Graham, Donald E. Knuth & Oren Patashnik: Concrete Mathematics - A Foundation for Computer Science. Addison-Wesley 1989.

[Hoare (1962)]

C. A. R. Hoare: Quicksort. Computer Journal 5(1962),10-15.

[Isaac (1956)]

E. J. Isaac & R. C. Singleton: Sorting by Address Calculation. Journal of the ACM 3(1956),169-174.

[Jonassen (1975)]

Arne Jonassen & Ole-Johan Dahl: Analysis of an Algorithm for Priority Queue Administration. BIT 15(1975),409-422.

[Knuth (1968)]

Donald E. Knuth: The Art of Computer Programming, vol I, Fundamental Algorithms Addison-Wesley 1973.

[Lueker (1980)]

George S. Lueker: Some Techniques for Solving Recurrences. Computing Surveys 12(1980), 419-436.

[Sedgewick (1978)]

Robert Sedgewick: Quicksort. Garland 1978.

[Sloane (1973)]

N. J. A. Sloane: A Handbook of Integer Sequences. Academic Press 1973.