Formler for forskellige lånetyper
Lån med konstant ydelse
Restgælden i termin nr. n må være:
Rn = Rn-1 - an
hvor an er afdraget i termin nr. n. Men afdraget i termin nr. n må være den konstante ydelse y minus renten i termin nr. n:
an = y - rn
Men renten i termin n må være:
rn = Rn-1i
hvor i er rentefoden. Heraf fås:
Rn = Rn-1 - y + rn = Rn-1 - y + Rn-1i = Rn-1(1+i) -y
Ved teleskopering fås nu:
Rn = (Rn-2(1+i) -y)(1+i) - y = Rn-2(1+i)2 - y(1+i) -y = ...![]()
Leddene i summen er en kvotientrække med kvotienten (1+i), og derfor bliver:
![]()
Rn er restgælden i termin nr. n, og R0 er restgælden til at begynde med, altså hovedstolen. Hvis vi sætter Rn til nul, har vi den situation, der eksisterer når lånet er betalt ud. Vi finder:
![]()
Heraf finder vi fx, at den nødvendige ydelse for et n-terminers lån på R0 er:
![]()
Jeg vil nu finde ud af, hvor meget man egentlig betaler i rente i hele lånets løbetid. Lad dette rentebeløb være R. Vi finder:
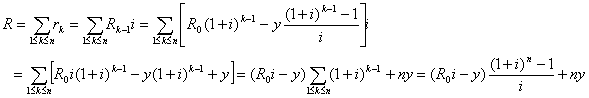
Da R0 kan udtrykkes ved y og i (jf. ovenfor) finder vi:
![]()
og R bliver derfor:
![]()
Den interessante størrelse er hvor stor en procentdel R er af hovedstolen (er det mon den størrelse man kalder "den effektive rente"?). Den bliver:
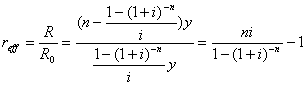
Lån med konstante afdrag
Restgæld efter n terminer:
Rn = Rn-1 - a = Rn-2 - 2a = ..... = R0 - na
Rente og ydelse i termin nr. n:
rn = Rn-1i = (R0 - (n-1)a)i
yn = rn + a = R0i - (n-1)ai + a
Når lånet er tilbagebetalt, er Rn = 0, og vi får den indlysende betingelse:
R0 = na
Den akkumulerede rente bliver:
![]()
eller, da R0 = na:
![]()
Heraf findes den effektive rente:
![]()
Kassekredit
I en kassekredit bliver renterne tilskrevet gælden, men man kan afdrage som man selv finder for godt. Jeg vil se på det simple tilfælde, hvor man afdrager med et bestemt beløb, a, hver termin. I dette tilfælde får man:
Rn = Rn-1 + rn - a
rn = Rn-1i
Disse ligninger er helt analoge til de tilsvarende ligninger i lån med konstant ydelse, hvor y blot er udskiftet med a. Det betyder at løsningerne for konstant ydelse kan overføres til denne lånetype ved at udskifte y med a. Vi finder derfor:
![]()
Hvis afdraget er for lille, vil en kassekredit aldrig blive afbetalt, men gælden vil vokse og vokse. Det kan derfor være af interesse at se, hvor stort afdraget skal være for at holde gælden konstant. Betingelsen er at Rn = Rn+1, eller:
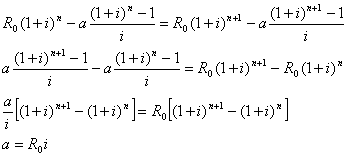
Afdraget skal altså være lig med renten i første termin (hvilket man jo kunne have sagt sig selv).
For at få gælden afviklet på n terminer, må afdraget være præcist så stort, at Rn = 0. Altså:
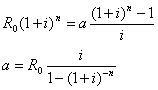
![]()
I tilfældet med konstant gæld bliver første led nul, og vi finder:
![]()
Den effektive rente er altså uafhængig af rentefoden, og vokser lineært med tiden.
Hvis afdraget er stort nok til af afvikle gælden på n terminer, bliver R lig med:
![]()
(jfr. analogien med annuitetslån) og vi finder:
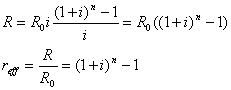
Hvis man ikke betaler af på sin kassekredit, fås R ved at sætte a til nul. Altså: