Lottomatematik

af

H. B. Hansen

 

I håb om at vinde den store gevinst er jeg begyndt at spille Lotto. For at vurdere mine chancer lavede jeg nogle beregninger over sandsynligheder i spillet. Dette essay handler om disse beregninger, som jeg til min overraskelse fandt var meget interessante i sig selv.

Lad mig til en begyndelse se på spillereglerne. På en lottokupon er der nogle "spilleplader", hver med 36 felter med tal fra 1 til 36. Man skal vælge  7 ud af de 36 tal på en spilleplade ved at sætte kryds i 7 af felterne. Det kaldes en række. Der findes også en anden slags kupon, kaldet en "systemkupon", hvor der kun er én spilleplade, men hvor man kan sætte flere end 7 krydser. Hvis man fx sætter 9 krydser har man spillet det antal rækker, som kan dannes ud fra disse 9 krydser.  Det er denne kupontype jeg anvender, så essayet handler om systemlotto.

En gang om ugen foretages en trækning, som består i at der udtrækkes 7 vindertal plus to såkaldte tillægstal. Der er gevinst i følgende tilfælde:

·        Man har gættet alle 7 vindertal (en række).

·        Man har 6 vindertal plus 1 tillægstal.

·        Man har 6 vindertal

·        Man har 5 vindertal.

·        Man har 4 vindertal.

Nu er det sådan at der også findes en anden slags lotto, "Onsdags lotto", hvor der er 48 felter på en spilleplade, men hvor en række til gengæld kun består af 6 krydser. Man får gevinst hvis man har 6 vindertal, 5 vindertal plus et tillægstal, 5 vindertal, 4 vindertal eller 3 vindertal.

Jeg vil gerne have et overblik over samtlige muligheder, og derfor generaliserer jeg problemet ved at indføre nogle parametre. Jeg spørger:

Hvad er sandsynligheden for at få r rigtige vindertal og s rigtige tillægstal hvis der er sat k krydser på en systemkupon i et lottospil med n felter på en kupon, hvis der er m vindertal og t tillægstal i en trækning?

I praksis vælger man jo de k krydser før de m vindertal og de t tillægstal er udtrukket. Jeg foretrækker imidlertid at anskue situationen om man så må sige omvendt: jeg tænker mig at m og t er kendt, og vi tækker i blinde k kugler fra en urne, der indeholder n nummererede kugler.

Det er vel ikke umiddelbart indlysende, at disse to forskellige situationer fører til de samme sandsynligheder,  men det tror jeg foreløbig på.

Først må jeg definere sandsynlighedsrummet for mit problem. Det er mængden af såkaldt "elementære" hændelser, der kan indtræffe, samt regler for tildeling af en sandsynlighed til hvert udfald af hændelsen. Det er vanskeligt at give en generel definition af en elementær hændelse, men i praksis er det sjældent så svært. Hvis man fx tænker på kast med en terning, så er selve kastet en elementær hændelse, der giver anledning til de elementære udfald, som er det antal øjne, terningen viser efter kastet. Der er altså 6 elementære udfald i dette tilfælde, og hvis det er en hel glat terning uden skævheder, og kastet udføres uden skjulte fiduser, så må man tillægge alle 6 udfald den samme sandsynlighed. Denne sandsynlighed skal være et tal mellem 0 og 1; 0 for et umuligt udfalde og 1 for et sikkert udfald.  At terningen skulle stå på højkant efter et kast anser jeg for et umuligt udfald (sandsynlighed 0). Det er derfor sikkert at terningen efter et kast viser enten 1, 2, 3, 4, 5 eller 6. Nu er det sådan at når udfaldene udelukker hinanden, som her, er sandsynligheden for "enten-eller" er lig med summen af de enkelte sandsynligheder. Derfor må hvert udfald tillægges sandsynligheden .

I lottoproblemet er den elementære hændelse udtrækningen af de k nummererede kugler, hvilket giver anledning til en mængde af elementære udfald i form af de mulige talsæt med k elementer, der kan fremkomme. Da udtrækningen er helt tilfældig tillægger jeg alle disse elementære udfald den samme sandsynlighed. Da summen af alle sandsynlighederne skal være 1, må hvert udfald tillægges en sandsynlighed, som er 1 divideret med antallet af elementære udfald. Det første delproblem i opgaven er derfor: hvad er antallet af elementære udfald?

Sagt på en anden måde: på hvor mange måder kan man udtrække k kugler af en urne med n kugler (uden tilbagelægning)?  Det er jo et standardproblem i den kombinatoriske matematik, så jeg kunne blot slå op i en lærebog og finde svaret. Men det er ikke nær så sjovt som at prøve at finde ud af det selv.

Den første kugle kan vælges på n måder; den lægger jeg på bordet. Nu trækker jeg en kugle til og lægger den ved siden af den første; det kan gøres på n-1 måder, for der er kun n-1 kugler tilbage i urnen. For hvert af de n udfald for den første kugle er der n-1 udfald for den anden; det samlede antal udfald for de to kugler er derfor n(n-1). Denne  tankerække udtrykker en meget fundamental kendsgerning, som man ofte møder i forbindelse med kombinatoriske problemer, og som kaldes produktreglen:

His en hændelse kan ske på m måder og en anden hændelse kan ske på n måder, så er der m*n måder hvorpå både den ene og den anden hændelse kan ske.

Der findes også en sumregel:

Hvis en hændelse kan ske på m måder og en anden hændelse kan ske på n måder, så er der m+n måder hvorpå enten den ene eller den anden hændelse kan ske.

Det er for øvrigt denne sumregel der ligger til grund for enten-eller reglen for sandsynligheder.

Produktreglen anvendt k gange på mit problem fører til, at man kan vælge k kugler ud af n på  n(n-1)(n-2)(n-3)...(n-k+1) forskellige måder.

Er det nu svaret på det oprindelige spørgsmål? Desværre nej! Problemet er at kuglerne på bordet ligger i en bestemt rækkefølge, nemlig den rækkefølge de blev valgt i. En hvilken som helst anden rækkefølge af de k kugler ville være lige så god. Det jeg har fundet er antallet af permutationer af k kugler valgt ud af n, hvilket dem der beskæftiger sig med denne form for matematik skriver således:

                  

Jeg er på jagt efter er det som matematikerne kalder antallet af kombinationer af k kugler ud af n. Det er det antal måder, hvorpå man kan vælge k ud af n uden hensyn til rækkefølgen. Dette antal, lad mig kalde det K(n,k), må være mindre end P(n,k), for hvis vi fx har fået valgt 3 kugler med numrene 1, 2 og 3 i denne rækkefølge, så vil rækkefølgerne {2,3,1}, {3,2,1}, {2,1,3}, {3,1,2} og {1,3,2} blive regnet for forskellige permutationer, men det er jo den samme kombination.

Nu laver jeg et tankeeksperiment. På bordet liggeren en kombination af k kugler. Nu bytter jeg om på dem på alle mulige måder; det kan gøres på P(k,k) måder (man kan nemlig forestille sig at de k kugler ligger i en sæk, som man trækker fra). Dette gentager jeg for alle K(n,k) kombinationer. For hver kombination kan der udføres P(k,k) permutationer, og når eksperimentet er færdigt, må alle de mulige permutationer være udført, altså P(n,k). Efter produktreglen må man derfor have:

eller:

                  

Nævneren i dette udtryk bliver k(k-1)(k-2)...3*2*1. Dette udtryk kaldes for fakultetsfunktionen af matematikerne og skrives k!. Funktionen er defineret for alle k større end eller lig med nul.  Det rejser spørgsmålet om, hvilken værdi fakultatsfunktionen skal have for værdien nul; her har matematikerne vedtaget, at 0! = 1. P(k,k) er altså lig med k!, så k elementer kan altså arrangeres på k! måder. Vi ser, at nul elementer altså matematisk set kan permuteres på 1 måde.

Udtrykket for K(n,k) kan skrives alene ved hjælp af fakultetsfunktionen. Det sker ved at forlænge brøken med (n-k)!:

              

Det var en lang vej for at komme frem til svaret på hvor mange elementære hændelser der er i sandsynlighedsrummet. Svaret blev K(n,k), og de har alle sandsynligheden .  Hvis n sættes til 36 og k sættes til 7, fås sandsynligheden for at få 7 rigtige i Lotto:

            

altså ca. 1 ud af 8 millioner, så udsigten til at jeg bliver rig fortoner sig lidt.

Nu spørger jeg mig selv: hvad er sandsynligheden for at få m rigtige med k krydser, når man ser bort fra tillægstal (kald denne sandsynlighed for p(m,k)). Det må være antallet af elementære hændelser med m rigtige ganget med sandsynligheden for hver af dem. De m rigtige kan naturligvis kun vælges på 1 måde, og så er der k-m kugler tilbage; og de må være valgt ud af den n-m "forkerte" kugler. Igen bruger jeg produktreglen og finder, at antallet af "gode" kombinationer er .

            

Svaret er defor:

           

Hvis jeg sætter n = 36 og m = 7 og k = 8 får jeg sandsynligheden for at få 7 rigtige på en systemkupon med 8 krydser til at være:

          

altså 8 gange så sandsynligt som at spille 1 række. Det er ikke så mærkeligt, for at sætte 8 krydser på en systemkupon betyder, at man spiller K(8,7) enkeltrækker, for det er det antal måder man kan vælge 7 ud af 8 på - og K(8,7) er lig med 8.

(Når man skal beregne værdien af K(n,k) hvor k er stor, så kan man benytte et trick, nemlig at K(n,k) må være lig med K(n,n-k). Det følger af at man kan vælge k elementer ud af n ved i stedet at specificere de n-k elementer der ikke skal vælges.  K(8,7) er derfor lig med K(8,1), som jo må være 8).

Som en kontrol af formlen for p(m,k) sætter jeg nu k = m. Det betyder nemlig at jeg kun spiller 1 række, og her kender jeg jo sandsynligheden fra tidligere. Jeg finder:

           

Her støder jeg altså på et mærkeligt problem: på hvor mange måder kan ingen elementer udtages af en given mængde? Skal det være 0 eller 1? Begge dele lyder plausibelt, men bemærk, at hvis værdien er 1, så får jeg det rigtige resultat  (fordi m = k), og det er da også hvad matematikerne er kommet frem til. De definerer at værdien af K(n,0) skal være 1 hvis n er større end eller lig med 0.

Så langt så godt.  Og nu tror jeg, tiden er moden til at se på tillægstallene også. Jeg laver igen et tankeeksperiment, hvor jeg først vælger r kugler, der skal være vindertal; de vælges ud af de m vindertal. Det kan gøres på K(m,r) måder. Dernæst vælger jeg s kugler ud af de t tillægstal på K(t,s) måder. Og til sidst vælges de "forkerte" kugler ud fra dem, der er til overs. Det giver et antal kombinationer på K(n-m-t,k-r-s). Produktreglen siger nu, at sandsynligheden p(r,s,k) bliver:




Kan det nu være rigtigt? En mulig fejlkilde ville være, at man beder om noget, der er umuligt. Fx om 7 rigtige og 2 tillægstal på en systemkupon med 8 krydser. Så siger formlen at sandsynligheden er:

           

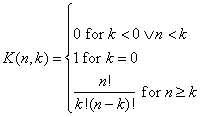
hvor spørgsmålstegnet giver udtryk for min usikkerhed om, hvad K(29,-1) betyder. Nu må jeg igen ty til matematikerne. De har heldigvis været så kloge at definere kombinationsfunktionen således:

          

så spørgsmålstegnet er lig nul, og hele sandsynligheden bliver nul.

Man hører ofte folk sige, at det må være lige så svært at få 0 rigtige som 7 rigtige i Lotto. Lad mig prøve.

           

Man får altså 0 rigtige og 0 tillægstal ca. hver 7'ende gang man spiller på en systemkupon med 8 krydser. Man skal ikke tro på alt hvad folk siger!

Foreløbig virker formlen jo meget overbevisende, men kan jeg nu være helt sikker på, at den er korrekt? En måde ville være at bruge den på et eksempel, som man kunne beregne på anden vis. Jeg har netop et eksempel fra tidligere, nemlig beregningen af sandsynligheden for at få m rigtige, når man ikke tager hensyn til tillægstal. Resultatet var:

          

Kan jeg mon komme frem til det samme ved at bruge den mere generelle formel, hvor tillægstallene jo er med?

Den simpleste måde er at sætte t = s = 0 i den generelle formel. Derved har jeg set bort fra begrebet tillægstal. Endvidere sætter jeg r = m, da jeg jo ønsker m rigtige. Herved fås:

          

hvilket stemmer.

Hvis man stadig ikke er overbevist om formlens rigtighed, kan man gå frem på en lidt anden måde. At man ser bort fra tillægstal må nemlig betyde, at man er ligeglad med om man får 0, 1, 2, ... eller t tillægstal. Men det vil sige at man kan lægge alle sandsynlighederne svarende til de t+1 tillægstalsituationer sammen (jfr. sumreglen). Jeg skal med andre ord finde summen:

          

Det ser jo stygt ud, men lad mig se på det. For det første er jeg interesseret i m rigtige, hvilket vil sige at r = m og derfor K(m,r) = K(m,m) = 1. Dernæst ser vi at K(n,k) ikke afhænger af summationsindekset s og derfor indgår som en konstant størrelse i alle led af S, så den må kunne sættes uden for summationstegnet (svarende til at sætte den uden for parentes). Alt ialt skal jeg altså beregne værdien af følgende sum:

         

og den skulle helst blive lig med K(n-m,k-m).

For at tackle denne opgave begynder jeg et tilsyneladende helt andet sted, nemlig i den del af matematiken, der handler om polynomier, specielt potenser af polynomier. Betragt det specielle polynomium:

Ved at gange parenteserne ud får man et polynomium af n'te grad ud af det:

Spørgsmålet er nu: hvor store er koefficienterne i dette polynomium?

Koefficienterne fås frem ved at gange faktorerene (1+x) med hinanden efter det kendte system med at gange hvert led i én af parenteserne med hvert led i en anden. Lad mig prøve med to faktorer: (1+x)(1+x). Konstanten a0, som egentlig er koefficienten til x0, fås ved at gange ettallet i første parentes med ettellet i anden parentes; altså er a0 = 1. Koefficienten til x fås ved at gange ettallet i første parentes med x'et i anden - og omvendt; derfor er  a1 = 2 Endelig fås koefficienten til x2 ved at gange de to x'er med hinanden, så a2 må være 1. Hvordan beregnes koefficienten til xk i det generelle tilfælde? Man skal selvfølgelig vælge x'et i k af faktorerne og ettellet i resten af faktorerene. Men at vælge x'et i k faktorer kan gøres på mange måder, nemlig på K(n,k) måder, og når først dette valg er truffet kan ettallerne kun vælges på 1 måde. Derfor må  ak = K(n,k), og vi kan konkludere at:

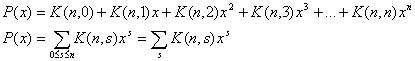
I sidste omskrivning har jeg droppet grænserne for s, og simpelthen summerer over alle mulige værdier af s (det vil sige fra -¥ til +¥).  Det kan man gøre fordi det der skal summeres bliver nul uden for intervallet fra 0 til n, jfr. definitionen af K(n,k) ovenfor.

Nu vil jeg prøve at finde koefficienten til xk i produktet af to polynomier, fx (1+x)u(1+x)v. Jeg identificerer koefficienterne i den første faktor med bogstavet a, og koefficienterne i den anden faktor med bogstavet b.

Koefficienten til xk kan nu findes ved først at gange ettallet i den første parentes med bkxk, derefter gange a1x1 med bk-1xk-1 og så fremdeles, indtil man når til akxk۠۠۠b0x0. Denne sum kan skrives således:

Koefficienten til xk er altså lig med  .

Bringer dette resultat mig nærmere til at finde summen S1 ? Ja, det gør det faktisk, for jeg ved jo at a’erne og b’erne er kombinationer. Koefficienten til xk kan derfor skrives:

            

Lad mig til sammenligning opskrive S1 nedenunder:

          

Det ligner jo meget, der er bare nogle andre betegnelser for de indgående størrelser samt nogle lidt forskellige grænser for summerne.

Hvad angår grænserne ses det, at begge summer bliver nul udenfor de anførte intervaller, så man kan simpelthen summere fra -∞ til +∞. Jeg kan derfor glemme alt om summationsgrænserne i begge summer.

Nu må det være sådan, at et matematisk udtryks værdi ikke kan afhænge af, hvad man kalder de indgående størrelser. Jeg foretager derfor nogle navneændringer i S2. I stedet for u skriver jeg t, i stedet for v skriver jeg n – m - t og i stedet for k skriver jeg k – m. Så bliver S2 identisk med S1.

Men nu kommer tricket: jeg kan nemlig finde S2 ud fra det udtryk, der skabte denne sum.  Jeg begyndte med udtrykket (1 + x)u(1 + x)v som jo må være lig med (1 + x)u+v, hvor koefficienten til xk jo må være K(u+v,k). Nu skal jeg passe lidt på, for jeg har erstattet k med k – m, så jeg skal faktisk finde koefficienten til xk-m. Derfor finder jeg:

og det ses at S1 får den forventede værdi.

Efter denne succes tror jeg på at den generelle formel for Lotto-lignende spil, formel (1) ovenfor, er korrekt.

 

Formel (1) er faktisk den generelle formel for fordelingsfunktionen af Lottospil. Jeg vil gerne se hvordan den ser ud og derfor fremstiller jeg et regneark. For ikke at komplicere  tingene for meget ser jeg bort fra tillægstal. Den formel jeg vil tabellægge ser derfor således ud:

hvor m er vindertallene,  r er antallet af rigtige på min lottokupon, n er antal tal i spillet (n = 36 for almindelig lotto) og k er antallet af krydser på kuponen (hvis m = k = 7 spiller jeg 1 række). Endvidere ser jeg bort fra nævneren i formlen, hvilket vil sige at jeg finder antallet af rækker med r rigtige for r = 0, 1, 2, …, m. Da nævneren resulterer i meget store tal tager jeg ydermere logaritmen til tallene for at få en nogenlunde skikkelig fordelingsfunktion frem. Den grafiske afbildning viser derfor det principielle forløb, mens man kan se de faktiske tal i tabellen. Du kan se resultatet af beregningerne  her: Lottofrekvenser.html