Talrækker i Lotto

af

H.B.Hansen

Jeg har lagt mærke til at der næsten altid forekommer et eller flere sæt nabotal i vinderkombinationen for Lottospillet. Til at begynde med undrede det mig meget, for ud fra en intuitiv betragtning ville jeg have gættet på at alle tallene i vinderkombinationen var spredt ud over hele det mulige interval og at der ganske vist ville optræde to tal i rækkefølge af og til, men ikke i næsten hver trækning. Men ved nærmere eftertanke er det måske ikke så mærkeligt.

Hvis man forestiller sig at der ikke var 36 tal at vælge imellem, men kun 12, så ville der med sikkerhed være mindst et par konsekutive tal i en vinderkombination på 7 tal. Hvis de 6 første tal nemlig var 1, 3, 5, 7, 9, 11, så ses det, at det syvende tal nødvendigvis må være nabotal til et af disse tal. Hvis der ikke var 12 tal at vælge ud fra, men fx 15, så ville forekomsten af nabotal være overordentlig sandsynlig. Spørgsmålet er nu: Hvad er sandsynligheden for forekomsten af nabotal i en vinderkombination på 7 tal, hvis disse vælges tilfældigt ud af 36 tal?

Det er dette spørgsmål jeg vil besvare i dette essay.

Første skridt i processen er at generalisere problemet, dvs. at indføre nogle betegnelser for de indgående størrelser. Hvis jeg regnede videre med tal, ville jeg uvægerligt komme til at foretage mellemregninger og derved blande de forskellige variable sammen og jeg ville ende med et eller andet tal. Det ville gøre mig ude af stand til at se det overordnede mønster og jeg måtte regne forfra hvis jeg fx ville finde sandsynligheden for nabotal i onsdags lotto i stedet for almindelig lotto. Det er bedre at finde en generel formel udtrykt ved de relevante variable. Opgaven lyder derfor således:

Hvad er sandsynligheden for forekomst af nabotal i en mængde af k tal valgt tilfældigt uden tilbagelægning fra en mængde af n forskellige tal?

Lad antallet af kombinationer uden nabotal af k tal valgt ud fra de n tal være f(n,k). Hvorfor vælger jeg nu at finde en formel for det der netop ikke spørges om? Det er fordi jeg har på fornemmelsen at denne funktion vil være lettere at beregne end den jeg er på jagt efter. Det er alt for mange specialtilfælde i nabotilfældet, fx 1 par, 2 par, 1 triple, 2 tripler, 4 tal i træk, osv. op til k tal i træk. I f(n,k) er der kun 2 specialtilfælde: kombinationen indeholder tallet 1 og/eller n (som kun har én nabo) eller kombinationen indeholder ikke disse tal (så er der to naboer). Og hvis jeg kender denne funktion er det let at finde den anden; den fås ved subtraktion mellem det samlede antal kombinationer og f(n,k).

Jeg vil først se på de tilfælde hvor hverken tallet 1 eller tallet n forekommer i kombinationen. Der er da n – 2 tal tilbage at fordele, og blandt dem skal man udvælge k tal på en sådan måde at der ikke er nogen nabotal. Det kan gøres på f(n-2,k) måder.

Dernæst ser jeg på de tilfælde, hvor tallet 1 forekommer i kombinationen, men tallet n ikke forekommer. Så kan vi forud vælge tallet 1 og anbringe det, men samtidig må vi udelukke tallene 2 (fordi 2 er nabotal til 1) og n. Nu skal vi udvælge k-1 tal ud fra de tilbageblevne n-3 tal . Det kan gøres på f(n-3,k-1) måder.

Det tilfælde hvor tallet n forekommer, men tallet 1 ikke forekommer, er helt analogt til det forrige tilfælde, så også her er der f(n-3,k-1) kombinationer.

Endelig er der det tilfælde hvor både 1 og n findes i kombinationen. Her kan disse to tal vælges på forhånd, men samtidig må deres nabotal udlukkes. Resutatet bliver at der er f(n-4,k-2) kombinationer.

Da disse fire tilfælde tilsammen udfylder alle muligheder fås, at f(n,k) må opfylde følgende funktionalligning (i det følgende kaldt for f-ligningen):

f(n,k) = f(n-2,k) + 2f(n-3,k-1) + f(n-4,k-2)

Opgaven består nu i at finde en funktion der tilfredsstiller denne ligning. Det ser unægtelig lidt stygt ud; der er tale om en rekursion med to variable, n og k, så de metoder jeg har benyttet i tidligere essays om kombinatorisk matematik kan ikke umiddelbart anvendes. I sådanne tilfælde kan man nogle gange komme helskindet igennem ved at gætte en løsning. Det vil jeg derfor prøve.

Jeg står imidlertid ikke helt på bar bund. Det er oplagt at gætte på en eller anden form for kombinatorisk funktion (og ikke fx på en trigonometrisk funktion), altså en funktion der udtrykker på hvor mange måder n objekter kan placeres i k positioner. Her har jeg i anden sammenhæng brugt funktionen K(n,k), der udtrykker netop dette hvis der ingen betingelser er. Her har vi imidlertid den betingelse der er udtrykt i f-ligningen og det medfører at parametrene i K-funktionen må modificeres på en eller anden måde.

Det er klart at størelserne n og k skal indgå i mit gæt og jeg mener også at der må være tale om lineære udtryk af n og k (det ville være mærkeligt hvis der fx pludselig optrådte et led med logaritmen til n). Det fører mig til følgende generelle gæt: K(an + bk + c, dk + e) hvor a,b c,d og e er visse konstanter, som jeg skal finde ved at påtrykke betingelsen i f-ligningen. Jeg har set bort fra en evt. afhængighed af n i anden parameter fordi jeg finder det højst usandsynligt, at n indgår her; anden parameter skal kun være afhængig af antallet af positioner, altså k.

Nu ved jeg at for k = 1 er der ingen kombinationer med nabotal (det er jo umuligt når der kun er 1 position). Men det vil sige at f(n,1) = K(an + b + c, d + e) må være lig med n (der er n kombinationer med kun ét tal). Det kan opnås hvis første parameter er n og anden parameter er 1, og jeg må derfor må derfor forlange at:

an + b + c = n

og:

d + e = 1

Her har jeg to ligninger med 5 ubekendte; det er jo ikke nok til at finde de ubekendte, så lad mig se mig om efter endnu en betingelse. Hvad med at prøve k = 2? Her er der n-1 kombinationer med nabotal, nemlig kombinationerne:

{1,2}, {2,3}, {3,4}, … ,{n-1,n}

men da man kan udvælge 2 ud af n tal på K(n,2) måder vil det sige at der er

kombintioner uden naboer. Men så er f(n,2) = K(an + 2b + c,2d + e) = K(n-1,2) og jeg må forlange at:

an + 2b + c = n – 1

og:

2d + e = 2

Nu har jeg fire ligninger med 5 ubekendte – det er da et skridt på vejen! De to sæt betingelser for d og e udgør to ligninger med 2 ubekendte, og det ses let at disse ligninger har løsningen {d,e} = {1,0}. Eftersom f(n,1) var lig med K(n,1) og f(n,2) var lig med K(n-1,2) gætter jeg på at a = 1. Nu bliver betingelser for a, b og c til 2 lignenger med 2 ubekendte, nemlig:

n + b + c = n

og:

n + 2b + c = n – 1

hvor n går ud og løsningen bliver {b,c} = {-1,1}. Mit gæt på en løsning til f-ligningen bliver altså:

f(n,k) = K(n – k + 1,k)

Men nu kommer den afgørende prøve, nemlig om K(n-k+1,k) passer ind i f-ligningen, eller sagt med andre ord, om højre side af f-ligningen kan reduceres til K(n-k+1,k). Jeg tager ét led ad gangen:

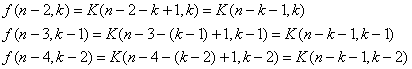
Herved kommer højre side af f-ligningen til at se sådan ud:

Dette udtryk må reduceres på en eller anden måde, for det skulle gerne ende med at blive K(n-k+1,k). Det jeg sådan umiddelbart kan finde på er at dele det midterste led i to og så parre disse to identiske led med hhv. første og sidste led:

Nu gælder der følgende formel for K-funktionen:

Det er den fundamentale additionsformel som følger af at hvis man fx maler et af de n elementer rødt, så må antallet af måder hvorpå man kan udvælge k elementer være lig med antallet med det røde element ekskluderet, , plus antallet med det røde element inkluderet, .

Nu kan jeg benytte denne formel på ovenstående udtryk og finder herved:

hvilket viser at min gættede løsning tilfredsstiller f-betingelsen.

Sandsynligheden for at vinderkombinationen ikke indeholder nabotal er derfor:

For almindelig lotto bliver denne sandsynlighed

og sandsynligheden for at der er mindst ét par er 1 - 0.24 = 0.76. Ikke mærkeligt at der næsten altid optræder nabotal i vinderkombinationerne!