af

Find antallet af inkongruente trekanter med heltallige sider og given perimeter.

Kald den givne perimeter n. Hvis siderne hedder a, b og c gælder det altså at a, b og c skal være hele tal og a + b + c = n. Heraf ses, at n er et helt tal. Det skader aldrig at se på nogle taleksempler; måske kan man finde et eller andet mønster der er værd af efterforske nærmere. Jeg får helt sikkert brug for at repræsentere en trekant på en eller anden måde, og da jeg helst vil undgå tegninger (det er for besværligt i Word) vælger jeg følgende repræsentation: {a,b,c}, hvor a ≥ b≥c.

Da en side må være større end nul ser vi, at der først kommer trekanter på bordet for n ≥ 3. Den første trekant er ligesidet med kantlængde 1: {1,1,1}. For n = 4 er der ingen trekanter. Den eneste mulighed ville være {2,1,1}, men det går ikke, for der gælder jo følgende betingelse: a < b + c for en trekant, og den er ikke opfyldt her. For n = 5 er der en enkelt trekant, nemlig {2,2,1}. Talfølgen for antallet af trekanter starter altså således: 0,0,0,1,0,1, ... Her er jo ikke meget at gå efter, så jeg må prøve nogle flere værdier af n. Efter en del kedeligt regneri og talmanipulation kom jeg frem til følgende tabel:

Jeg kan ikke umiddelbart se noget system i antal-kolonnen, som jo indeholder starten af den talfølge, jeg er på jagt efter - bortset fra, at der er flere trekanter for den ulige værdi n end for den lige værdi n-1. Derfor gav jeg mig til at stirre på mængden af trekanter (den midterste søjle i tabellen), for om muligt at finde en redning her.

Da jeg havde gloet på trekanterne i tabellen en rum tid opdagede jeg, at mange af trekanterne hang sammen i et simpelt system. Det er nemlig sådan, at hvis trekanten {a,b,c} findes i tabellen, så vil trekanten {a+1,b+1,c+1} også være der. Det er sådan set indlysende, for hvis a < b + c, så vil det også gælde at a +1 < (b+1) + (c+1). Reglen er altså generel og ikke blot et heldigt tilfælde i den begrænsede tabel. Men det betyder, at man kan finde nogle af trekanterne for perimeter n ved at se på antallet for perimeter n-3, eller mere formelt:

hvor f(n) er en eller anden endnu ukendt funktion af n. Nu er problemet reduceret til at finde f(n).

Det fremgår af tabellen, at for ulige værdier af n er der gennemgående flere trekanter end for lige værdier. Det skyldes, at man for ulige n kan have trekanter, hvor den mindste side har værdien 1, mens dette ikke er muligt for lige værdier af n. Hvis nemlig den længste side er m, så må den næstlængste være m-1 når den mindste skal være 1; så er perimeteren ganske rigtigt et lige tal, 2m, men betingelsen a < b + c er ikke opfyldt.

Det er klart, at for ulige n kan man altid danne en trekant af formen Herefter kan man gradvis formindske den næststørste side og forstørre den mindste; herved finder man alle trekanter med længste side Men hvor mange gange kan man gøre det? Det kan vi finde ud af ved hjælp af følgende trekant: hvor p går fra nul og op - men kun sålænge Ved at løse denne ligning med hensyn til p fås og det søgte antal bliver Antallet må naturligvis være et helt tal, men 4 går ikke altid op selv om n + 1 jo er et lige tal (prøv fx n = 5). Vi må derfor skrive:

Antal trekanter med længste side (for ulige n) er , hvor betyder største heltal .

Nu tager jeg fat på at finde antallet af trekanter for ulige n med største side mindre end Lad mig prøve med trekanten hvor q er ulige og n ≥ 3. Jeg vil vise, at denne trekant er efterkommer af en, der allerede findes i forvejen for et mindre n. Derfor trækker jeg 1 fra hver af siderne og finder perimeteren af denne nye trekant. Altså:

Med andre ord: trekantens "forgænger" findes blandt trekanterne med perimeter n - 3. De eneste "nye" trekanter er dem med q = 1 som korteste side. Dette argument gælder også hvis n og q er lige, og jeg slutter heraf, at der aldrig genereres "nye" trekanter for lige værdier af n.

Men nu har jeg faktisk fundet funktionen f(n), og kan opskrive et par rekursioner for antallet af trekanter:

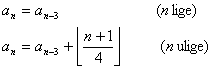
med startværdierne a₀ = a₁ = a₂ = 0.

Men virker det mon? Jeg prøver de første led i tralfølgen, blot for at være sikker:

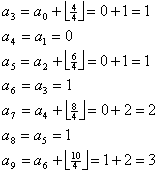
Det ser rigtig godt ud, så det tror jeg på. Nu er det let at finde antallet af trekanter, fx ved hjælp af et program (her er ét i Pascal):

program trekanter;
  var n,i,k: word;
      a: array [0..3] of word;
begin
  write('Perimeter: '); readln(n);
  a[0] := 0; a[1] := 0; a[2] := 0;
  for i := 3 to n do begin
    k := i mod 2;
    case k of
       0: a[3] := a[0];
       1: a[3] := a[0] + (i+1) div 4
    end;
    for k := 0 to 2 do a[k] := a[k+1]
  end;
  writeln('Der er ',a[3],' trekanter med perimeter ',n)
end.

Dette program gav det rigtige resultat for alle 0 ≤ n ≤ 13. Det er selvfølgelig ikke nogen særlig udtømmende test, men det er heller ikke programmet, jeg er interesseret i. Jeg vil hellere bruge energi på at finde et sluttet udtryk for antallet af trekanter; så kan jeg fx se hvor hurtigt antallet stiger med n.

Hvor det n'te led skal være antallet af inkongruente trekanter med perimeter n. Jeg kender allerede starten af denne potensrække, specielt at de tre første led er nul, og så kender jeg en sammenhæng mellem leddene, udtrykt ved den rekursion, jeg udledte i forrige afsnit. Uheldigvis er der to sammenhørende rekursioner, en for lige værdier af n og en for ulige. Det vil derfor sikkert være en fordel at se på de lige og de ulige led i A(x) hver for sig. De lige led kan isoleres ved at danne følgende funktion:

Lad mig kalde denne funktion for A_lige(x). Den analoge funktion A_ulige(x) findes ved at danne [A(x) - A(-x)].

Nu kan jeg give mig i kast med de to rekursioner. Problemet er åbenbart her at udtrykke A_lige(x) ved A_ulige(x) og omvendt. De to frembringerfunktioner skal forskydes tre pladser mod venstre, så a₃ bliver til a₀ osv. Her vil jeg benytte mig af et matematiker-trick, nemlig at definere alle uegentlige led til venstre for a₀ i en frembringerfunktion (dvs. alle de negative potenser af x) til at være nul. Det betyder nemlig, at jeg kan summere over alle værdier af n ( ), og jeg behøver derfor ikke at bekymre mig om grænserne for summerne. Lad mig først se, hvad der sker hvis jeg ganger en vilkårlig frembringerfunktion, G(z), med z³?

hvor den sidste omskrivning fremkommer ved at udskifte n med n-3 i næstsidste udtryk. Det er klart at den potens man ganger med lige så godt kan være 4, 5, eller et vilkårligt heltal, m, så her har vi en generel regel til at forskyde en frembringerfunktion m pladser til venstre.

Nu kan jeg gange de to rekursioner med xⁿ og summere over n og herved jeg finder et udtryk for A(x):

hvor:

Hvis jeg adderer disse to ligninger får jeg:

Med andre ord: hvis jeg kan finde S(x) har jeg samtidig fundet A(x).

Jeg kan ikke lide den såkaldte "gulvfunktion", der optræder i S(x). Den er vanskelig at have med at gøre i summationer. Derfor vil jeg nu forsøge at afskaffe den. Det jeg ved er, at n er ulige, og derfor erstatter jeg n med 2d - 1. Nu bliver gulvfunktionen:

Heraf ses, at hvis 2 går op i d (som må være lig med (n+1)/2), så går 4 op i n+1, og hvis d/2 giver resten 1, så giver (n+1)/4 også resten 1, og 4 går derfor op i n-1. Vi kan derfor slippe af med gulvfunktionen ved at skrive:

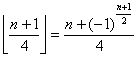
Det var så farvel til den gulvfunktion!

Så er det tid at tage livtag med S(x). Den første vanskelighed er at summen kun løber over ulige værdier af n, men det kan jeg klare ved at erstatte n med 2n+1:

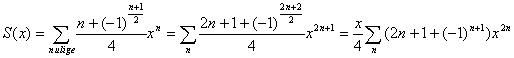
Dette udtryk kan omformes til:

hvor:

Nu tager jeg fat på de tre summer, én ad gangen. Jeg begynder med den letteste:

Her er nemlig tale om en uendelig kvotientrække med kvotienten z (dvs. , hvor n går mod uendelig og z vælges passende). Summen er let at klare, selv om den ser lidt styg ud:

Det er nemlig en kvotientrække med kvotient -z. Den største udfordring ligger i summen Lad os se lidt nærmere på den. Den følgende beregning går ud på, først at integrere, og derefter differentiere en udvalgt del af frembringerfunktionen. På den måde kan man nemlig finde summen. Se blot her:

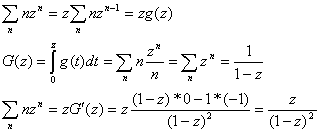
Denne beregning viser en af styrkerne i anvendelse af frembringerfunktioner. Da alle beregninger er formelle, kan man integrere og differentiere næsten efter forgodtbefindende. Nu har jeg fundet T(z):

som efter nogle banale omskrivninger kan reduceres til:

Herefter kan jeg finde S(x):

og (endelig) frembringerfunktionen for inkongruente trekanter, A(x):

Dette udtryk har en overraskende simpel form og det vil nok være klogt at undersøge, om det kan være rigtigt. Da 1/(1-z) jo er summen af en uendelig kvotientrække med kvotienten z, må 1/(1-x^m) være summen af en uendelig kvotientrække med kvotient x^m. Derfor fås:

Koefficienterne til xⁿ fremkommer ved at vælge ét led fra hver af faktorerne, således at potenssummen netop bliver n. Fx fås koefficienten til x¹¹ således:

Som man ser stemmer potensrækken med den tabel, jeg opstillede i begyndelsen af dette essay. For yderligere sikkerhed prøver jeg nu at køre programmet for rekursionerne med en ny værdi af n. Jeg vælger n = 21 fordi det så ikke bliver uoverkommeligt at finde koefficienten til x²¹ (det ville det være hvis jeg fx valgte n = 117). Jeg vil tro på min frembringerfunktion hvis der er overensstemmelse mellem disse to beregninger. Kørslen med Pascalprogrammet gav følgende udskrift:

Jeg vil nu konstruere en tabel med 4 søjler, hvor der i hver række står de potenser fra frembringerfunktionen, der skal til for at få netop summen 21. Antallet af rækker skulle så gerne blive 12.

I tabellen er der ganske rigtigt 12 rækker, og jeg kan ikke finde flere kombinationer, der giver summen 21. Men er det nu ikke bare mig, der kludrer i det? Her jeg ikke ubevidst ladet mig lokke til at stoppe min søgning efter nye kombinationer, da jeg nåede til 12? For at komme denne nagende tvivl til livs skrev jeg et program (i Prolog) der fandt alle kombinationerne. Det ser således ud:

  frembring :-
     anden(U),member(A,U),tredie(V),member(T,V),
     fjerde(L),member(F,L),X is 3+A+T+F,X =:= 21,
     writelist([3,A,T,F]),fail.
  frembring :- write('Det var det hele!'),nl.

  anden([0,2,4,6,8,10,12,14,16,18,20]).
  tredie([0,3,6,9,12,15,18,21]).
  fjerde([0,4,8,12,16,20]).

  writelist([X]) :- write(X),nl,!.
  writelist([X|L]) :- write(X),write(', '),writelist(L).

  member(X,[X|_]).
  member(X,[_|L]) :- member(X,L).

Prædikatet frembring bruger den såkaldte "generate-and-test" strategi til at generere kombinationer af de potenser, der står i prædikaterne anden, tredie og fjerde; når en kombination med summen 21 mødes, udskrives den, og der backtrackes. Som generator bruges prædikatet member.

En kørsel med programmet gav følgende resultat:

| ?- frembring.
3, 0, 6, 12
3, 0, 18, 0
3, 2, 0, 16
3, 2, 12, 4
3, 4, 6, 8
3, 6, 0, 12
3, 6, 12, 0
3, 8, 6, 4
3, 10, 0, 8
3, 12, 6, 0
3, 14, 0, 4
3, 18, 0, 0
Det var det hele! 

Der er de samme kombinationer i dette resultat som i den manuelle tabel, blot i en anden rækkefølge. Herefter tror jeg på, at A(x) er den korrekte frembringerfunktion.

Hele denne aktivitet har fået mig til at se en overraskende sammenhæng mellem antallet af inkongruente trekanter med given perimeter, og opsplitning af hele tal i addender. Tabellen ovenfor indeholder jo de mulige opsplitninger af tallet 21, idet der kun anvendes multipla af 2, 3 og 4 og tallet 3 forekommer mindst én gang i hver opsplitning. Hvilken relation har det til frembringerfunktionen? Ser vi på udviklingen i potensrækker kan man sige, at et 1-tal i den første parentes (egentlig x⁰) svarer til ingen 2-taller, x² svarer til ét 2-tal, x⁴ svarer til to 2-taller, ..., x²ⁿ svarer til n 2-taller, og analogt for de to andre parenteser. Det enlige x³ betyder, at der altid er mindst ét 3-tal (man kunne jo gange det ind i anden parentes, så forsvinder 1-tallet og alle potenser forøges med 3).

Hvis jeg gentager min tabel og tilføjer opsplitningerne, ses det måske tydeligere (jeg skriver addenderne i stigende rækkefølge):

Jeg har hermed bevist følgende sætning:

Ved løsning af denne opgave har altså jeg til min egen overraskelse fundet frembringerfunktionen for opsplitning af hele tal. Hvis vi dropper faktoren x³ fås frembringerfunktionen for opsplitning af et heltal i addenderne 2, 3 og 4:

Dette resultat kan generaliseres. Funktionen:

må således være frembringerfunktion for opsplitning af et heltal i addender ≤ m, og:

er den generelle frembringerfunktion for opsplitning af de hele tal.

Det var min mening at finde et sluttet udtryk for antallet af inkongruente trekanter med heltallige sider og given perimeter, et udtryk der kan beregnes med en lommeregner. Det er ikke lykkedes. Jeg har fundet et sæt rekursioner og en frembringerfunktion, der hver for sig genererer det ønskede antal, men kun ved hjælp af omfattende beregninger, der kræver brug af computer. Til gengæld har jeg opdaget en ikke-indlysende sammenhæng mellem antal trekanter og opsplitning af hele tal. Det er da noget. Jeg vil gå videre og forsøge at løse rekursionerne uden brug af frembringerfunktioner. Det vil måske give mig de ønskede formler. Men det bliver en anden gang!